题目内容
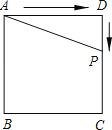
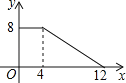
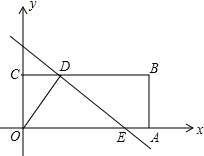
【题目】如图，在矩形OABC中，点A、C的坐标分别为（10，0），（0，2），点D是线段BC上的动点（与端点B、C不重合），过点D作直线y=﹣
x+m交线段OA于点E．
（1）矩形OABC的周长是 ；
（2）连结OD，当OD=DE时，求m的值；
（3）若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1，试探究四边形O1A1B1C1与矩形OABC重叠部分的面积是否会随着E点位置的变化而变化，若不变，求出该重叠部分的面积；若改变，请说明理由．
【答案】（1）24；（2）m=4；（3）矩形O1A1B1C1与矩形OABC重叠部分的面积不会随着点E位置的变化而变化，且面积始终为5．
【解析】
试题分析：（1）根据点A、C的坐标可得出线段OA、OC的长，再根据矩形的周长公式即可得出结论；
（2）根据直线DE的解析式可得出点D、E的坐标，再根据等腰三角形的性质可得出OE=2CD，从而得出关于m的一元一次方程，解方程即可得出结论；
（3）设O1A1与CB相交于点M，OA与C1B1相交于点N，过点D作DH⊥OA于点H，由此得出矩形O1A1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积．
根据对称的性质可得出四边形DNEM为平行四边形，再根据平行线的性质可找出∠MED=∠MDE，从而得出四边形DNEM为菱形，设该菱形的边长为a，通过在RT△DHN中利用勾股定理求出a的值，再根据菱形的面积公式求出S菱形DNEM为定值即可得出结论．
解：（1）∵在矩形OABC中，点A、C的坐标分别为（10，0），（0，2），
∴AB=OC=2，BC=OA=10，
∴C矩形OABC=（OC+OA）×2=24．
故答案为：24．
（2）令y=﹣
x+m中y=0，则﹣x+m=0，
解得：x=2m，即点E（2m，0）；
令y=﹣x+m中y=2，则﹣x+m=2，
解得：x=2m﹣4，即点D（2m﹣4，2）．
∵OD=DE，四边形OABC为矩形，
∴OE=2CD，即2m=2×（2m﹣4），
解得：m=4．
（3）设O1A1与CB相交于点M，OA与C1B1相交于点N，过点D作DH⊥OA于点H，如图所示．
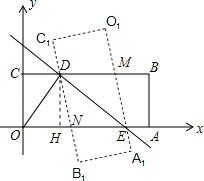
矩形O1A1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积．
由题意知：DM∥NE，DN∥ME，
∴四边形DNEM为平行四边形．
根据轴对称知，∠MED=∠NED，
∵DM∥NE，
∴∠MDE=∠NED，
∴∠MED=∠MDE，
∴MD=ME，
∴平行四边形DNEM为菱形．
∵OC=2，
∴DH=2，
∵直线DE的解析式为y=﹣
x+m，
∴HE=2DH=4．
设菱形DNEM 的边长为a，
∴HN=HE﹣NE=OE﹣OH﹣NE=4﹣a，
在RT△DHN中，（4﹣a）2+22=a2，
解得：a=
，
∴S菱形DNEM=NEDH=5，
∴矩形O1A1B1C1与矩形OABC重叠部分的面积不会随着点E位置的变化而变化，且面积始终为5．
