题目内容
已知抛物线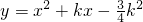 (k为常数,且k>0).
(k为常数,且k>0).
(1)证明:此抛物线与x轴总有两个交点;
(2)设抛物线与x轴的两个交点分别是M、N.
①M、N两点之间的距离为MN=______.(用含k的式子表示)
②若M、N两点到原点的距离分别为OM、ON,且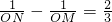 ,求k的值.
,求k的值.
证明:(1)∵△=k2-4×1×(- k2)=4k2,
k2)=4k2,
∵k>0,
∴△>0,
∴抛物线与x轴总有两个交点;
(2)①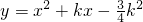 =0,
=0,
解得:x1=-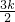 ,x2=
,x2= ,
,
∴MN= -(-
-(-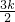 )=2k;
)=2k;
②∵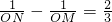 >0,
>0,
∴ON<OM,
∴ON= ,OM=
,OM=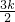 ,
,
∴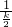 -
-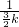 =
= ,
,
解得k=2.
分析:(1)由判别式△>0即可证明;
(2)①由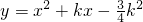 =0,解得:x1=-
=0,解得:x1=-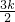 ,x2=
,x2= ,即可得出答案;
,即可得出答案;
②由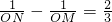 >0,可得ON<OM,所以ON=
>0,可得ON<OM,所以ON= ,OM=
,OM=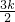 ,即可得出答案.
,即可得出答案.
点评:本题考查了二次函数综合题,难度一般,关键是掌握用判别式△>0证明抛物线与x轴总有两个交点.
 k2)=4k2,
k2)=4k2,∵k>0,
∴△>0,
∴抛物线与x轴总有两个交点;
(2)①
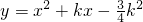 =0,
=0,解得:x1=-
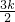 ,x2=
,x2= ,
,∴MN=
 -(-
-(-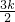 )=2k;
)=2k;②∵
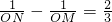 >0,
>0,∴ON<OM,
∴ON=
 ,OM=
,OM=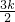 ,
,∴
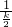 -
-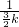 =
= ,
,解得k=2.
分析:(1)由判别式△>0即可证明;
(2)①由
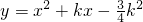 =0,解得:x1=-
=0,解得:x1=-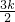 ,x2=
,x2= ,即可得出答案;
,即可得出答案;②由
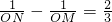 >0,可得ON<OM,所以ON=
>0,可得ON<OM,所以ON= ,OM=
,OM=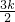 ,即可得出答案.
,即可得出答案.点评:本题考查了二次函数综合题,难度一般,关键是掌握用判别式△>0证明抛物线与x轴总有两个交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 :
: (
( 为常数,且
为常数,且 )的顶点为
)的顶点为 ,与
,与 轴交于点
轴交于点 ;抛物线
;抛物线 与抛物线
与抛物线 。若点
。若点 是抛物线
是抛物线 (B)、
(B)、 (C)、
(C)、 (D)、
(D)、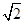
 :
: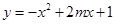 (
( 为常数,且
为常数,且 )的顶点为
)的顶点为 ,与
,与 轴交于点
轴交于点 ;抛物线
;抛物线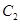 与抛物线
与抛物线 .若点
.若点 是抛物线
是抛物线
 B.
B. C.
C. D.
D.
 :
: (
( 为常数,且
为常数,且 )的顶点为
)的顶点为 ,与
,与 轴交于点
轴交于点 ;抛物线
;抛物线 与抛物线
与抛物线 。若点
。若点 是抛物线
是抛物线 B.
B. C.
C. D.
D.