题目内容
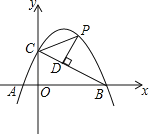
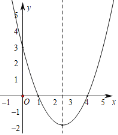
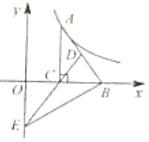
【题目】如图已知抛物线y＝﹣x2+（1﹣m）x﹣m2+12交x轴于点A，交y轴于点B（0，3），顶点C位于第二象限，连接AB，AC，BC．
（1）求抛物线的解析式；
（2）在x轴上是否存在点P，使得△PAB的面积等于△ABC的面积？如果存在，求出点P的坐标．
（3）将△ABC沿x轴向右移动t个单位长度（0＜t＜1）时，平移后△ABC和△ABO重叠部分的面积为S，求S与t之间的函数关系．
【答案】（1）y＝﹣x2﹣2x+3；（2）点P的坐标为（﹣1，0）或（﹣5，0）；（3）
【解析】
（1）利用二次函数图象上点的坐标特征可求出m的值，结合抛物线的顶点在第二象限可得出m＞1，进而可确定m的值，再将其代入抛物线解析式中即可得出结论；
（2）过点C作CD⊥x轴，垂足为点D，利用二次函数图象上点的坐标特征及配方法，可求出点A，C的坐标，利用分割图形求面积法可求出△ABC的面积，再由三角形的面积公式结合S△PAB＝S△ABC可求出AP的长，结合点A的坐标，即可求出点P的坐标；
（3）设△ABC平移后得到△A′B′C′，A′B′与y轴交于点M，A′C′交AB于点N，根据点的坐标，利用待定系数法可求出线段AB，AC所在直线的解析式，结合平移的性质可得出线段A′B′，A′C′所在直线的解析式，利用一次函数图象上点的坐标特征可求出点M，N的坐标，由三角形、梯形的面积公式结合S＝S△AOB﹣S△AA′N﹣S△AA′M，即可得出S关于t的函数关系式．
（1）∵抛物线y＝﹣x2+（1﹣m）x﹣m2+12交y轴于点B（0，3），
∴﹣m2+12＝3，
∴m＝±3．
又∵抛物线的顶点C位于第二象限，
∴﹣
，
∴m＞1，
∴m＝3，
∴抛物线的解析式为y＝﹣x2﹣2x+3．
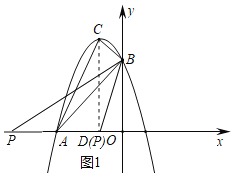
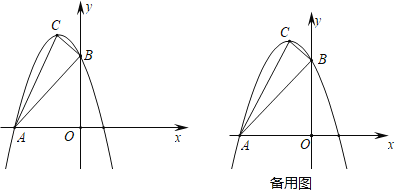
（2）过点C作CD⊥x轴，垂足为点D，如图1所示．
当y＝0时，﹣x2﹣2x+3＝0，
解得：x1＝﹣3，x2＝1，
∴点A的坐标为（﹣3，0）．
∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，
∴点C的坐标为（﹣1，4），点D的坐标为（﹣1，0），
∴S△ABC＝S△ACD+S梯形CDOB﹣S△AOB，
＝
ADCD+（OB+CD）OD﹣OAOB，
＝×2×4+×（3+4）×1﹣×3×3，
＝3．
∵S△PAB＝S△ABC，
∴APOB＝3，
∴AP＝2，
∴点P的坐标为（﹣1，0）或（﹣5，0）．
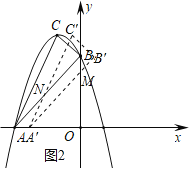
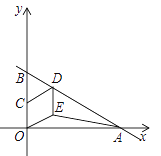
（3）设△ABC平移后得到△A′B′C′，A′B′与y轴交于点M，A′C′交AB于点N，如图2所示．
设线段AB所在直线的解析式为y＝kx+b（k≠0），
将A（﹣3，0），B（0，3）代入y＝kx+b，得：
，解得：
，
∴线段AB所在直线的解析式为y＝x+3．
同理，可得出线段AC所在直线的解析式为y＝2x+6．
∵将△ABC沿x轴向右移动t个单位长度（0＜t＜1）得到△A′B′C′，
∴点A′的坐标为（t﹣3，0），线段A′B′所在直线的解析式为y＝x+3﹣t（0＜t＜1），线段A′C′所在直线的解析式为y＝2x+6﹣2t（0＜t＜1）．
当x＝0时，y＝x+3﹣t＝3﹣t，
∴点M的坐标为（0，3﹣t）．
将y＝x+3代入y＝2x+6﹣2t，整理，得：x+3﹣2t＝0，
解得：x＝2t﹣3，
∴点N的坐标为（2t﹣3，2t），
∴S＝S△AOB﹣S△AA′N﹣S△AA′M，
＝OAOB﹣AA′yA′﹣OA′OM，
＝×3×3﹣t2t﹣（3﹣t）（3﹣t），
＝﹣
t2+3t．
∴S与t之间的函数关系式为S＝﹣ t2+3t（0＜t＜1）．
