Question

阅读并填空：
在小学的时候，我们通过剪纸发现了三角形三个内角间的关系．你还记得吗？
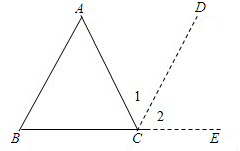
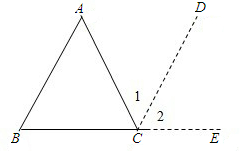
已知：如图△ABC，∠A、∠B、∠C之和为多少？为什么？
解：∠A+∠B+∠C=180°
理由：过点C作CD∥AB，∴∠1=∠A（________ ）∠B=∠2（________）
而∠ACB+∠1+________=180°（平角的定义 ）∴∠ACB+∠B+∠A=180°（________）

Answer 1

两直线平行，内错角相等    两直线平行，同位角相等    ∠2    等量代换
分析：过点C作CD∥AB，推出∠1=∠A，∠2=∠B，代入∠ACB+∠1+∠2=180°即可求出答案．
解答：过点C作CD∥AB，
则∠1=∠A（两直线平行，内错角相等），
∠2=∠B（两直线平行，同位角相等），
∵∠ACB+∠1+∠2=180°，
∴∠A+∠B+∠ACB=180°（等量代换），
故答案为：两直线平行，内错角相等，两直线平行，同位角相等，∠2，等量代换．
点评：本题考查了平行线的性质，注意：两直线平行，内错角相等，两直线平行，同旁内角互补