题目内容
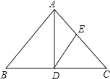
【题目】如图,在△ABC中,∠C=150°,AC=4,tanB=![]() .
.
(1)求BC的长;
(2)利用此图形求tan15°的值(精确到0.1,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2).
≈2.2).
![]()
【答案】(1)BC=16-2![]() ;(2) tan15°≈0.3.
;(2) tan15°≈0.3.
【解析】
(1)作AD⊥BC交BC的延长线于D,分别在Rt△ACD,Rt△ADB中求出CD,BD即可解决问题;
(2)在CB上取一点M,使得CM=CA,连接AM,则∠AMC=15°,在Rt△ADM中,根据tan15°==tan∠AMD=![]() 计算即可解决问题.
计算即可解决问题.
(1)过点A作AD⊥BC,交BC的延长线于点D,如图①所示.
![]()
在Rt△ADC中,AC=4.
∵∠ACB=150°,∴∠ACD=30°,
∴AD=![]() AC=2,
AC=2,
CD=AC·cos30°=4×![]() =2
=2![]() .
.
在Rt△ABD中,tanB=![]() ,
,
∴BD=16,
∴BC=BD-CD=16-2![]() .
.
(2)在BC边上取一点M,使得CM=AC,连接AM,如图②所示.

∵∠ACB=150°,∴∠AMC=∠MAC=15°,
tan15°=tan∠AMD=![]() ≈
≈![]() ≈0.3.
≈0.3.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目