题目内容
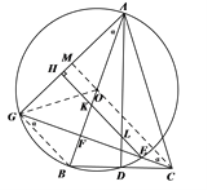
【题目】已知:AB是⊙0直径,C是⊙0外一点,连接BC交⊙0于点D,BD=CD,连接AD、AC.
(1)如图1,求证:∠BAD=∠CAD
(2)如图2,过点C作CF⊥AB于点F,交⊙0于点E,延长CF交⊙0于点G.过点作EH⊥AG于点H,交AB于点K,求证AK=2OF;
(3)如图3,在(2)的条件下,EH交AD于点L,若0K=1,AC=CG,求线段AL的长.

图1 图2 图3
【答案】(1)见解析(2)见解析(3) ![]()
【解析】试题分析:(1)由直径所对的圆周角等于90°,得到∠ADB=90°,再证明△ABD≌△ACD即可得到结论;
(2)连接BE.由同弧所对的圆周角相等,得到∠GAB=∠BEG.再证△KFE≌△BFE,得到BF=KF=![]() BK.由OF=OB-BF,AK=AB-BK,即可得到结论.
BK.由OF=OB-BF,AK=AB-BK,即可得到结论.
(3)连接CO并延长交AG于点M,连接BG.设∠GAB= ![]() .先证CM垂直平分AG,得到AM=GM,∠AGC+∠GCM=90°.再证∠GAF=∠GCM =
.先证CM垂直平分AG,得到AM=GM,∠AGC+∠GCM=90°.再证∠GAF=∠GCM = ![]() .通过证明△AGB≌△CMG,得到BG=GM=
.通过证明△AGB≌△CMG,得到BG=GM=![]() AG.再证明∠BGC=∠MCG=
AG.再证明∠BGC=∠MCG= ![]() .设BF=KF=a,
.设BF=KF=a, ![]() GF=2a,AF=4a.
GF=2a,AF=4a.
由OK=1,得到OF=a+1,AK=2(a+1),AF= 3a+2,得到3a+2=4a,解出a的值,得到AF,AB,GF,FC的值.由tanα=tan∠HAK=![]() , AK=6,可以求出 AH的长.再由
, AK=6,可以求出 AH的长.再由![]() ,利用公式tan∠GAD=
,利用公式tan∠GAD=![]() ,得到∠GAD=45°,则AL=
,得到∠GAD=45°,则AL=![]() AH,即可得到结论.
AH,即可得到结论.
试题解析:解:(1)∵AB为⊙O的直径,∴∠ADB=90°,∴∠ADC=90°.
∵BD=CD,∠BDA=∠CDA,AD=AD,∴△ABD≌△ACD,∴∠BAD=∠CAD.
(2)连接BE.∵BG=BG ,∴∠GAB=∠BEG.
∵CF⊥AB,∴∠KFE=90°.
∵EH⊥AG,∴∠AHE=∠KFE=90°,∠AKH=∠EKF,∴∠HAK=∠KEF=∠BEF.
∵FE=FE,∠KFE=∠BFE=90°,∴△KFE≌△BFE,∴BF=KF=![]() BK.
BK.
∵ OF=OB-BF,AK=AB-BK,∴AK=2OF.

(3)连接CO并延长交AG于点M,连接BG.设∠GAB= ![]() .
.
∵AC=CG, ∴点C在AG的垂直平分线上.∵ OA=OG,∴点O在AG的垂直平分线上,
∴CM垂直平分AG,∴AM=GM,∠AGC+∠GCM=90°.
∵AF⊥CG,∴∠AGC +∠GAF =90°,∴∠GAF=∠GCM = ![]() .
.
∵AB为⊙O的直径,∴∠AGB= 90°,∴∠AGB=∠CMG=90°.
∵AB=AC=CG ,∴△AGB≌△CMG,∴BG=GM=![]() AG.
AG.
在Rt△AGB中, ![]() .
.
∵∠AMC=∠AGB= 90°,∴BG∥CM, ∴∠BGC=∠MCG= ![]() .
.
设BF=KF=a, ![]() ,∴GF=2a,
,∴GF=2a, ![]() ,AF=4a.
,AF=4a.
∵OK=1,∴OF=a+1,AK=2OF=2(a+1),∴AF=AK+KF=a+2(a+1)=3a+2,∴3a+2=4a,∴a=2, AK=6,∴AF=4a=8,AB=AC=CG=10,GF=2a=4,FC=CG-GF=6.
∵tanα=tan∠HAK=![]() ,设KH=m,则AH=2m,∴AK=
,设KH=m,则AH=2m,∴AK=![]() =6,解得:m=
=6,解得:m=![]() ,∴AH=2m=
,∴AH=2m=![]() .在Rt△BFC中,
.在Rt△BFC中, ![]() .∵∠BAD+∠ABD=90°, ∠FBC+∠BCF=90°,∴∠BCF=∠BAD,
.∵∠BAD+∠ABD=90°, ∠FBC+∠BCF=90°,∴∠BCF=∠BAD, ![]() ,∴tan∠GAD=
,∴tan∠GAD=![]() =
= ,∴∠GAD=45°,∴HL=AH,AL=
,∴∠GAD=45°,∴HL=AH,AL=![]() AH=
AH= ![]() .
.


【题目】为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.

(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | 方差 | |
一班 | a | b | 90 | 106.24 |
二班 | 87.6 | 80 | c | 138.24 |
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.



