题目内容
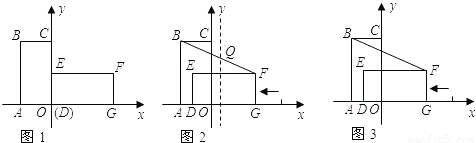
(2008•随州)在平面直角坐标系中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=1,OC=2.将矩形OABC绕点O顺时针旋转90°,得到矩形DEFG(如图1).(1)若抛物线y=-x2+bx+c经过点B和F,求此抛物线的解析式;
(2)将矩形DEFG以每秒1个单位长度的速度沿x轴负方向平移,平移t秒时,所成图形如图2所示.
①图2中,在0<t<1的条件下,连接BF,BF与(1)中所求抛物线的对称轴交于点Q,设矩形DEFG与矩形OABC重合部分的面积为S1,△AQF的面积为S2,试判断S1+S2的值是否发生变化?如果不变,求出其值;
②在0<t<3的条件下,P是x轴上一点,请你探究:是否存在t值,使以PB为斜边的Rt△PFB与Rt△AOC相似?若存在,直接写出满足条件t的值及点P的坐标;若不存在,请说明理由(利用图3分析探索).
【答案】分析:(1)首先确定点B、F的坐标,将点的坐标代入函数解析式,解方程组即可求得;
(2)①首先求得对称轴,根据题意用t表示出S1、S2的值即可求得.
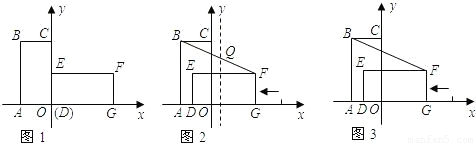
②利用相似三角形的性质即可求得:过点F作FP⊥FB,FP交x同于点P,延长FE交AB于点M,
要使Rt△PFB∽Rt△AOC,只要FB:FP=2:1即可,而Rt△BMF∽Rt△PGF,所以根据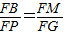 只须
只须 ,列出方程解答即可求出此时点P的坐标.
,列出方程解答即可求出此时点P的坐标.
解答:解:(1)B(-1,2),F(2,1)
∵抛物线y=-x2+bx+c经过点B和F,
∴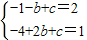
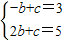
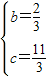
所求抛物线y=-x2+ (3分)
(3分)
(2)①如图,连接AQ,AF,延长FE交AB于点M,
由题意得:OD=t,FM=3-t,
(1)中所求抛物线的对称轴为直线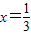 (4分)
(4分)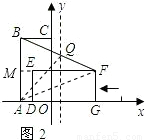
∴S1=DE•OD=t(5分)
S2=S△AFB-S△AQB= •2•(3-t)-
•2•(3-t)- •2•
•2• ,
,
即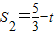
∴S1+S2=
S1+S2的值不变(7分)
②存在满足题意的t值,t1=1,t2= ,此时点P的坐标为(
,此时点P的坐标为( ,0)及(-
,0)及(- ,0)(12分)
,0)(12分)
(说明:写出一个t值及对应的点P坐标,给3分)
下面给出求t值及点P坐标的一种思路,供参考.如图1,
过点F作FP⊥FB,FP交x同于点P,延长FE交AB于点M,
要使Rt△PFB∽Rt△AOC,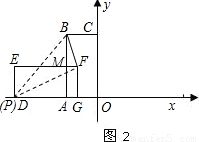
只要FB:FP=2:1,
而Rt△BMF∽Rt△PGF,
∴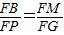
只须 ,即3-t=2,t=1
,即3-t=2,t=1
此时点P的坐标为
要使Rt△PFB∽Rt△AOC,只要FB:FP=1:2,
同理只须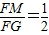 ,
,
即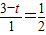 ,
,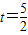 ,
,
此时矩形DEFG所在位置如图2所示,点P的坐标为(- ,0).
,0).
∴t1=1, ,
,
故点P的坐标为( ,0)及(-
,0)及(- ,0).
,0).
点评:此题考查了二次函数与四边形的综合知识,解题时要仔细审题,理解题意;特别是要注意数形结合思想与方程思想的应用.
(2)①首先求得对称轴,根据题意用t表示出S1、S2的值即可求得.
②利用相似三角形的性质即可求得:过点F作FP⊥FB,FP交x同于点P,延长FE交AB于点M,
要使Rt△PFB∽Rt△AOC,只要FB:FP=2:1即可,而Rt△BMF∽Rt△PGF,所以根据
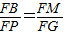 只须
只须 ,列出方程解答即可求出此时点P的坐标.
,列出方程解答即可求出此时点P的坐标.解答:解:(1)B(-1,2),F(2,1)
∵抛物线y=-x2+bx+c经过点B和F,
∴
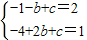
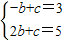
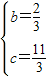
所求抛物线y=-x2+
 (3分)
(3分)(2)①如图,连接AQ,AF,延长FE交AB于点M,
由题意得:OD=t,FM=3-t,
(1)中所求抛物线的对称轴为直线
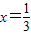 (4分)
(4分)
∴S1=DE•OD=t(5分)
S2=S△AFB-S△AQB=
 •2•(3-t)-
•2•(3-t)- •2•
•2• ,
,即
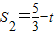
∴S1+S2=

S1+S2的值不变(7分)
②存在满足题意的t值,t1=1,t2=
 ,此时点P的坐标为(
,此时点P的坐标为( ,0)及(-
,0)及(- ,0)(12分)
,0)(12分)(说明:写出一个t值及对应的点P坐标,给3分)
下面给出求t值及点P坐标的一种思路,供参考.如图1,
过点F作FP⊥FB,FP交x同于点P,延长FE交AB于点M,
要使Rt△PFB∽Rt△AOC,

只要FB:FP=2:1,
而Rt△BMF∽Rt△PGF,
∴
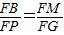
只须
 ,即3-t=2,t=1
,即3-t=2,t=1此时点P的坐标为

要使Rt△PFB∽Rt△AOC,只要FB:FP=1:2,
同理只须
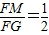 ,
,即
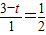 ,
,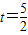 ,
,此时矩形DEFG所在位置如图2所示,点P的坐标为(-
 ,0).
,0).∴t1=1,
 ,
,故点P的坐标为(
 ,0)及(-
,0)及(- ,0).
,0).点评:此题考查了二次函数与四边形的综合知识,解题时要仔细审题,理解题意;特别是要注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
(2008•随州)某生物科技发展公司投资2000万元,研制出一种绿色保健食品.已知该产品的成本为40元/件,试销时,售价不低于成本价,又不高于180元/件.经市场调查知,年销售量y(万件)与销售单位x(元/件)的关系满足下表所示的规律.
(1)y与x之间的函数关系式是______,自变量x的取值范围为______;
(2)经测算:年销售量不低于90万件时,每件产品成本降低2元,设销售该产品年获利润为W(万元)(W=年销售额-成本-投资),求出年销售量低于90万件和不低于90万件时,W与x之间的函数关系式;
(3)在(2)的条件下,当销售单位定为多少时,公司销售这种产品年获利润最大?最大利润为多少万元?
| 销售单价x(元/件) | … | 60 | 65 | 70 | 80 | 85 | … |
| 年销售量y(万件) | … | 140 | 135 | 130 | 120 | 115 | … |
(2)经测算:年销售量不低于90万件时,每件产品成本降低2元,设销售该产品年获利润为W(万元)(W=年销售额-成本-投资),求出年销售量低于90万件和不低于90万件时,W与x之间的函数关系式;
(3)在(2)的条件下,当销售单位定为多少时,公司销售这种产品年获利润最大?最大利润为多少万元?