题目内容
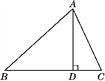
【题目】已知△ABC中，其最小的内角∠C=24°，过顶点B的一条直线把这个三角形分割成了两个等腰三角形，则∠ABC=_____．
【答案】117°或108°
【解析】
根据题意作图，根据等腰三角形的性质分情况讨论即可求解.
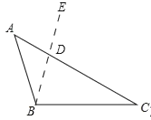
①如图，∠C=24°
依题意可得∠DBC=∠BDC=
=78°，
故∠ABD=∠BAD=
∠BDC=39°，
∴∠ABC=∠ABD+∠DBC=117°，
∠A=180°-∠C-∠ABC=39°，
符合最小的内角为∠C=24°，
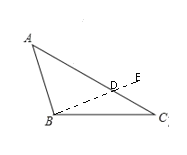
②如图，∠C=24°
依题意可得∠DBC=∠C=24°，
故∠ADB=2∠C=48°，
∴∠A=∠ADB =48°，
∠ABD=180°-∠A-∠ADB =84°，
∴∠ABC=∠ABD+∠DBC=108°，
符合最小的内角为∠C=24°，
综上，∠ABC=117°或108°
故填：117°或108°.
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】某商场试销一种成本为每件
元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于
，经试销发现，销售量
（件）与销售单价
（元）符合一次函数，所调查的部分数据如表：
销售单价 | 60 | 65 | 70 |
|
销售量 | 60 | 55 | 50 |
|
（1）求出与之间的函数表达式；
（2）若该商场获得利润为
元，试写出利润与销售单价之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少？
（3）销售单价定为多少元时，该商场获得的利润恰为
元？
