题目内容
如图①,P是线段AB上一点,△APC与△BPD是等边三角形(三边相等,三个角都为60°的三角形).
(1)请你判断:AD与BC相等吗?并说明理由;
(2)如图②,若△BPD绕P点旋转一定角度,(1)中的结论还成立吗?
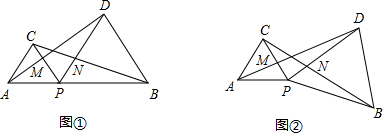
解:(1)AD=BC,理由:
∵△APC和△BPD都是等边三角形,
∴∠APC=∠DPB=∠CPD=60°,
∴∠APC+∠CPD=∠DPB+∠CPD,
在△APD和△CPB中,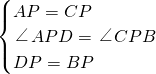 ,
,
∴△APD≌△CPB(SAS),
∴AD=BC(全等三角形对应边相等);
(2)条件改变,结论仍然成立.
∵△APC和△BPD都是等边三角形,
∴∠APC=∠DPB=∠CPD=60°,
∴∠APC+∠CPD=∠DPB+∠CPD,
∴∠APD=∠CPB,
在△APC和△BPD中,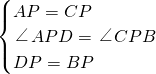 ,
,
∴△APD≌△CPB(SAS),
∴AD=BC(全等三角形对应边相等).
分析:(1)根据等边三角形的性质利用SAS即可判定△APD和△CPB,根据全等三角形的对应边相等即可证得AD=BC.
(2)结论仍然成立,用类例(1)的方法证△APD和△CPB,再根据全等三角形的性质即可得到结论.
点评:此题主要考查学生对全等三角形的判定及性质和等边三角形的性质的综合运用能力.得到∠APD=∠CPB是正确解答本题的关键.
∵△APC和△BPD都是等边三角形,
∴∠APC=∠DPB=∠CPD=60°,
∴∠APC+∠CPD=∠DPB+∠CPD,
在△APD和△CPB中,
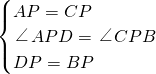 ,
,∴△APD≌△CPB(SAS),
∴AD=BC(全等三角形对应边相等);
(2)条件改变,结论仍然成立.
∵△APC和△BPD都是等边三角形,
∴∠APC=∠DPB=∠CPD=60°,
∴∠APC+∠CPD=∠DPB+∠CPD,
∴∠APD=∠CPB,
在△APC和△BPD中,
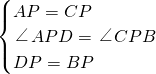 ,
,∴△APD≌△CPB(SAS),
∴AD=BC(全等三角形对应边相等).
分析:(1)根据等边三角形的性质利用SAS即可判定△APD和△CPB,根据全等三角形的对应边相等即可证得AD=BC.
(2)结论仍然成立,用类例(1)的方法证△APD和△CPB,再根据全等三角形的性质即可得到结论.
点评:此题主要考查学生对全等三角形的判定及性质和等边三角形的性质的综合运用能力.得到∠APD=∠CPB是正确解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点C是线段AB的黄金分割点,则下列等式不正确的是( )
如图,点C是线段AB的黄金分割点,则下列等式不正确的是( )A、
| ||||
B、
| ||||
C、AC=
| ||||
D、BC=
|
 4、如图,直线l是线段AB的垂直平分线,则下列结论:①OA=OB,②l⊥AB,③PA=PB,④∠A=∠B中,
4、如图,直线l是线段AB的垂直平分线,则下列结论:①OA=OB,②l⊥AB,③PA=PB,④∠A=∠B中, 8、如图,点C是线段AB上一点,以AB、AC为边在AB的同侧作正方形,设AC=2,BC=x,则阴影部分的面积是( )
8、如图,点C是线段AB上一点,以AB、AC为边在AB的同侧作正方形,设AC=2,BC=x,则阴影部分的面积是( ) (2012•北碚区模拟)已知:如图,点C是线段AB的中点,CD∥BE,∠D=∠E,求证:CD=BE.
(2012•北碚区模拟)已知:如图,点C是线段AB的中点,CD∥BE,∠D=∠E,求证:CD=BE. 如图,点C是线段AB的中点,AB=6cm,如果点D是线段AB上一点,且BD=1cm,那么CD=
如图,点C是线段AB的中点,AB=6cm,如果点D是线段AB上一点,且BD=1cm,那么CD=