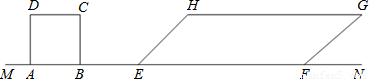
题目内容
正方形ABCD与平行四边形EFGH的AB、EF在同一条直线MN上,AB=2cm,EF=6cm,BE=2cm,∠HEF=45°,EH=2 cm,正方形ABCD以1cm/s速度向右移动,在移动过程中两图形重叠部分的面积为Scm2.试探索在不同时间内的面积S(设右移时间为t秒).
cm,正方形ABCD以1cm/s速度向右移动,在移动过程中两图形重叠部分的面积为Scm2.试探索在不同时间内的面积S(设右移时间为t秒).
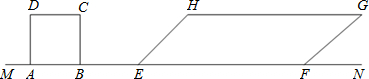
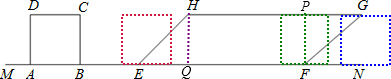 解:分别作HQ⊥EF于Q,PF⊥HG于P.
解:分别作HQ⊥EF于Q,PF⊥HG于P.∴sin45°=
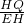 ,
,∵EH=2
 ,
,∴HQ=2,
∴EQ=2,
∵四边形EFGH是平行四边形,
∴PG=PF=2,QF=HP=4,
∴由题意得
当2≤t<4时,
S1=
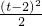 =
=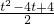 ;
;当4≤t<6时
S2=4-
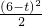 =
=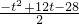 ;
;当6≤t<8时,
S3=4;
当8≤t<10时,
S4=4-
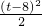 =
=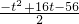 ;
;当10≤t≤12时,
S5=
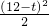 =
=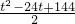 .
.分析:过点H作HQ⊥EF与点Q,利用解直角三角形可以求出HQ=EQ的长度,就是平行四边形的高,与正方形的边长相等,将正方形点B在EQ间和点C在PG间移动和点A在EQ间及点D在PG间移动时正方形与平行四边形重合的面积的5种情况分别表示出来即可.
点评:本题是一道动点问题的函数试题,考查了平行四边形的性质,正方形的性质,平移的性质,要求学生进行分段求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
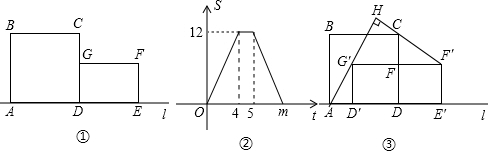
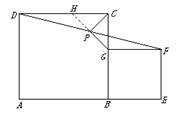 25、请阅读下列材料:
25、请阅读下列材料: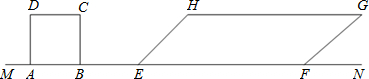
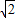 cm,正方形ABCD以1cm/s速度向右移动,在移动过程中两图形重叠部分的面积为Scm2.试探索在不同时间内的面积S(设右移时间为t秒).
cm,正方形ABCD以1cm/s速度向右移动,在移动过程中两图形重叠部分的面积为Scm2.试探索在不同时间内的面积S(设右移时间为t秒).