题目内容
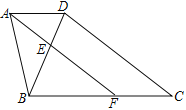
【题目】如图，广场中心菱形花坛ABCD的周长是32米，∠A＝60°，则A、C两点之间的距离为（ ）
A. 4米 B. 
米 C. 8米 D. 
米
【答案】D
【解析】由四边形ABCD为菱形，得到四条边相等，对角线垂直且互相平分，将问题转化为求OA；根据∠BAD=60°得到△ABD为等边三角形，即可求出OB的长，再利用勾股定理求出OA即可求解.
设AC与BD交于点O.
∵四边形ABCD为菱形，
∴AC⊥BD，OA=OC，OB=OD，AB=BC=CD=AD=32÷4=8米.
∵∠BAD=60°，AB=AD，
∴△ABD为等边三角形，
∴BD=AB=8米，
∴OD=OB=4米.
在Rt△AOB中，根据勾股定理得：OA=4
（米），
∴AC=2OA=8米.
故选D.
练习册系列答案
相关题目
【题目】阅读下列材料：
有这样一个问题：关于x 的一元二次方程a x2+bx+c=0（a＞0）有两个不相等的且非零的实数根．探究a，b，c满足的条件．
小明根据学习函数的经验，认为可以从二次函数的角度看一元二次方程，下面是小明的探究过程：
①设一元二次方程ax2+bx+c=0（a＞0）对应的二次函数为y=ax2+bx+c（a＞0）；
②借助二次函数图象，可以得到相应的一元二次中a，b，c满足的条件，列表如下：
方程根的几何意义：请将（2）补充完整
方程两根的情况 | 对应的二次函数的大致图象 | a，b，c满足的条件 |
方程有两个 不相等的负实根 |
|
|
_____ |
|
|
方程有两个 不相等的正实根 | _____ | _____ |
（1）参考小明的做法，把上述表格补充完整；
（2）若一元二次方程mx2﹣（2m+3）x﹣4m=0有一个负实根，一个正实根，且负实根大于﹣1，求实数m的取值范围．
