题目内容
已知:如图,抛物线y=ax2+bx+c的顶点C在以D(-2,-2)为圆心,4为半径的圆上,且经过⊙D与x轴的两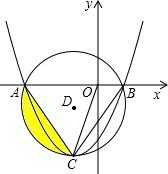 个交点A、B,连接AC、BC、OC.
个交点A、B,连接AC、BC、OC.(1)求点C的坐标;
(2)求图中阴影部分的面积;
(3)在抛物线上是否存在点P,使DP所在直线平分线段OC?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)作CH⊥x轴,垂足为H,CH必经过圆心D,易得CH=6,则点C的坐标可以得到.
(2)连接OA,OC则阴影部分的面积S=S扇形DAC-S△DAC;
(3)设OC的中点是E,E点的坐标就可以求出,利用待定系数法就可以求出直线DE的解析式,直线与抛物线的交点就是所求的点P.
(2)连接OA,OC则阴影部分的面积S=S扇形DAC-S△DAC;
(3)设OC的中点是E,E点的坐标就可以求出,利用待定系数法就可以求出直线DE的解析式,直线与抛物线的交点就是所求的点P.
解答: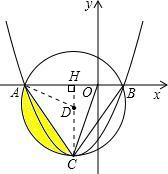 解:(1)如图,作CH⊥x轴,垂足为H,
解:(1)如图,作CH⊥x轴,垂足为H,
∵直线CH为抛物线对称轴,
∴CH垂直平分AB,
∴CH必经过圆心D(-2,-2).
∵DC=4,
∴CH=6
∴C点的坐标为(-2,-6).(3分)
(2)连接AD.
在Rt△ADH中,AD=4,DH=2,
∴∠HAD=30°,AH=
=2
(4分)
∴∠ADC=120°
∴S扇形DAC=
=
π(5分)
S△DAC=
AH•CD=
×2
×4=4
.(6分)
∴阴影部分的面积S=S扇形DAC-S△DAC=
π-4
.(7分)
(3)又∵AH=2
,H点坐标为(-2,0),H为AB的中点,
∴A点坐标为(-2-2
,0),B点坐标为(2
-2,0).(8分)
又∵抛物线顶点C的坐标为(-2,-6),
设抛物线解析式为y=a(x+2)2-6.
∵B(2
-2,0)在抛物线上,
∴a(2
-2+2)2-6=0,
解得a=
.
∴抛物线的解析式为y=
(x+2)2-6(9分).
设OC的中点为E,过E作EF⊥x轴,垂足为F,连接DE,
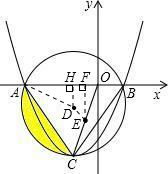 ∵CH⊥x轴,EF⊥x轴,
∵CH⊥x轴,EF⊥x轴,
∴CH∥EF
∵E为OC的中点,
∴EF=
CH=3,OF=
OH=1.
即点E的坐标为(-1,-3).
设直线DE的解析式为y=kx+b(k≠0),
∴
,
解得k=-1,b=-4,
∴直线DE的解析式为y=-x-4.(10分)
若存在P点满足已知条件,则P点必在直线DE和抛物线上.
设点P的坐标为(m,n),
∴n=-m-4,即点P坐标为(m,-m-4),
∴-m-4=
(m+2)2-6,
解这个方程,得m1=0,m2=-6
∴点P的坐标为(0,-4)和(-6,2).
故在抛物线上存在点P,使DP所在直线平分线段OC.(12分)
 解:(1)如图,作CH⊥x轴,垂足为H,
解:(1)如图,作CH⊥x轴,垂足为H,∵直线CH为抛物线对称轴,
∴CH垂直平分AB,
∴CH必经过圆心D(-2,-2).
∵DC=4,
∴CH=6
∴C点的坐标为(-2,-6).(3分)
(2)连接AD.
在Rt△ADH中,AD=4,DH=2,
∴∠HAD=30°,AH=
| AD2-DH2 |
| 3 |
∴∠ADC=120°
∴S扇形DAC=
| 120°×π×42 |
| 360° |
| 16 |
| 3 |
S△DAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴阴影部分的面积S=S扇形DAC-S△DAC=
| 16 |
| 3 |
| 3 |
(3)又∵AH=2
| 3 |
∴A点坐标为(-2-2
| 3 |
| 3 |
又∵抛物线顶点C的坐标为(-2,-6),
设抛物线解析式为y=a(x+2)2-6.
∵B(2
| 3 |
∴a(2
| 3 |
解得a=
| 1 |
| 2 |
∴抛物线的解析式为y=
| 1 |
| 2 |
设OC的中点为E,过E作EF⊥x轴,垂足为F,连接DE,
 ∵CH⊥x轴,EF⊥x轴,
∵CH⊥x轴,EF⊥x轴,∴CH∥EF
∵E为OC的中点,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
即点E的坐标为(-1,-3).
设直线DE的解析式为y=kx+b(k≠0),
∴
|
解得k=-1,b=-4,
∴直线DE的解析式为y=-x-4.(10分)
若存在P点满足已知条件,则P点必在直线DE和抛物线上.
设点P的坐标为(m,n),
∴n=-m-4,即点P坐标为(m,-m-4),
∴-m-4=
| 1 |
| 2 |
解这个方程,得m1=0,m2=-6
∴点P的坐标为(0,-4)和(-6,2).
故在抛物线上存在点P,使DP所在直线平分线段OC.(12分)
点评:本题主要考查了待定系数法求函数的解析式,以及弓形面积的求法,转化为扇形的面积与三角形的面积的差的问题.

练习册系列答案
相关题目
 与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.
与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A( 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0). 已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.
已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.