题目内容
【题目】如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则以AC和BC的长为两根的一元二次方程是 . 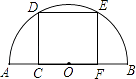
【答案】此题答案不唯一,如:x2﹣ ![]() x+1=0
x+1=0
【解析】解:连接AD,BD,OD, 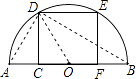
∵AB为直径,
∴∠ADB=90°,
∵四边形DCFE是正方形,
∴DC⊥AB,
∴∠ACD=∠DCB=90°,
∴∠ADC+∠CDB=∠A+∠ADC=90°,
∴∠A=∠CDB,
∴△ACD∽△DCB,
∴ ![]() ,
,
又∵正方形CDEF的边长为1,
∵ACBC=DC2=1,
∵AC+BC=AB,
在Rt△OCD中,OC2+CD2=OD2 ,
∴OD= ![]() ,
,
∴AC+BC=AB= ![]() ,
,
以AC和BC的长为两根的一元二次方程是x2﹣ ![]() x+1=0.
x+1=0.
所以答案是:此题答案不唯一,如:x2﹣ ![]() x+1=0.
x+1=0.
【考点精析】掌握根与系数的关系和勾股定理的概念是解答本题的根本,需要知道一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目