题目内容
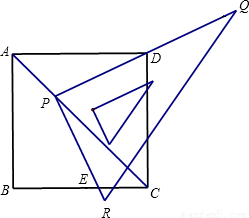
如图所示,在边长为1的正方形ABCD中,一直角三角尺PQR的直角顶点P在对角线AC上移动,直角边PQ经过点D,另一直角边与射线BC交于点E.(1)试判断PE与PD的大小关系,并证明你的结论;
(2)连接PB,试证明:△PBE为等腰三角形;
(3)设AP=x,△PBE的面积为y,
①求出y关于x 函数关系式;
②当点P落在AC的何处时,△PBE的面积最大,此时最大值是多少?
【答案】分析:(1)作辅助线:过点P作GF∥AB,分别交AD、BC于G、F,构建全等三角形Rt△EFP≌Rt△PGD(ASA),然后由全等三角形的对应边相等证明PE=PD;
(2)由正方形的四条边相等,对角线平分对角的性质证明△APB≌△APD(SAS),然后由全等三角形的对应边相等证明PB=PD;利用(1)的结论,由等量代换证明PE=PB,即△PBE为等腰三角形;
(3)①利用△APB≌△APD的对应边相等知,BF=PG.在直角三角形AGP中,利用边角关系求得BF=PG的值,所以PF=AB-GP;然后根据三角形的面积公式求得关于y与x的函数关系式;
②根据①的函数关系式y=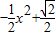 x的顶点式函数关系式求最值.
x的顶点式函数关系式求最值.
解答:证:(1)过点P作GF∥AB,分别交AD、BC于G、F.如图所示.
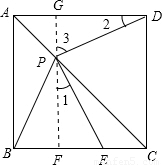
∵四边形ABCD是正方形,
∴四边形ABFG和四边形GFCD都是矩形,△AGP和△PFC都是等腰直角三角形,
∴GD=FC=FP,GP=AG=BF,∠PGD=∠PFE=90°;
又∵∠1+∠3=∠2+∠3=90°,
∴∠1=∠2;
又PF=GD,∠PFE=∠PGD=90°,
∴Rt△EFP≌Rt△PGD(ASA),
∴PE=PD;
(2)∵AD=AB,∠PAB=∠PAD=45°,AP=AP,
∴△APB≌△APD(SAS),
∴PB=PD,
∴PE=PB,
∴△PBE为等腰三角形;
(3)①∵AP=x,
∴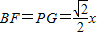 ,
,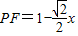 ,
,
∴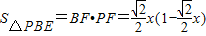 =
=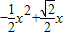 .
.
即 (
(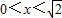 ),
),
②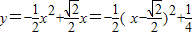 .
.
∵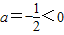 ,
,
∴当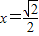 时,
时, .
.
点评:本题综合考查了二次函数的最值、正方形的性质、等腰三角形的性质及全等三角形的判定与性质.解答此题的关键是通过作辅助线:过点P作GF∥AB,分别交AD、BC于G、F,构建全等三角形Rt△EFP≌Rt△PGD(ASA),另外在求二次函数的最值时,在初中阶段一般情况下是将函数的一般解析式转化为顶点式函数解析式,然后根据函数的性质求其解析式.
(2)由正方形的四条边相等,对角线平分对角的性质证明△APB≌△APD(SAS),然后由全等三角形的对应边相等证明PB=PD;利用(1)的结论,由等量代换证明PE=PB,即△PBE为等腰三角形;
(3)①利用△APB≌△APD的对应边相等知,BF=PG.在直角三角形AGP中,利用边角关系求得BF=PG的值,所以PF=AB-GP;然后根据三角形的面积公式求得关于y与x的函数关系式;
②根据①的函数关系式y=
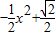 x的顶点式函数关系式求最值.
x的顶点式函数关系式求最值.解答:证:(1)过点P作GF∥AB,分别交AD、BC于G、F.如图所示.

∵四边形ABCD是正方形,
∴四边形ABFG和四边形GFCD都是矩形,△AGP和△PFC都是等腰直角三角形,
∴GD=FC=FP,GP=AG=BF,∠PGD=∠PFE=90°;
又∵∠1+∠3=∠2+∠3=90°,
∴∠1=∠2;
又PF=GD,∠PFE=∠PGD=90°,
∴Rt△EFP≌Rt△PGD(ASA),
∴PE=PD;
(2)∵AD=AB,∠PAB=∠PAD=45°,AP=AP,
∴△APB≌△APD(SAS),
∴PB=PD,
∴PE=PB,
∴△PBE为等腰三角形;
(3)①∵AP=x,
∴
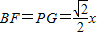 ,
,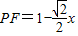 ,
,∴
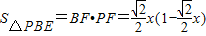 =
=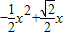 .
.即
 (
(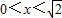 ),
),②
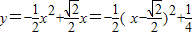 .
.∵
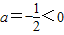 ,
,∴当
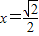 时,
时, .
.点评:本题综合考查了二次函数的最值、正方形的性质、等腰三角形的性质及全等三角形的判定与性质.解答此题的关键是通过作辅助线:过点P作GF∥AB,分别交AD、BC于G、F,构建全等三角形Rt△EFP≌Rt△PGD(ASA),另外在求二次函数的最值时,在初中阶段一般情况下是将函数的一般解析式转化为顶点式函数解析式,然后根据函数的性质求其解析式.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
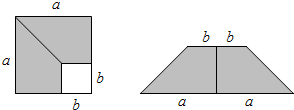

| A、(a-b)2=a2-2ab+b2 | B、(a+b)2=a2+2ab+b2 | C、a2-b2=(a+b)(a-b) | D、a2+ab=a(a+b) |

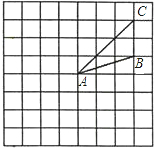 如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′,并计算对应点B和B′之间的距离.
如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′,并计算对应点B和B′之间的距离. 如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.
如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.