题目内容
【题目】双蓉服装店老板到厂家购A、B两种型号的服装，若购A种型号服装6件，B种型号服装16件，需要1260元；若购进A种型号服装12件，B种型号服装8件，需要1080元。
（1）求A、B两种型号的服装每件分别为多少元？
（2）若销售一件A型服装可获利20元，销售一件B型服装可获利30元，根据市场需要，服装店老板决定：购进A型服装的数量要比购进B型服装的数量的2倍还多4件，且A型服装最多可购进28件，这样服装全部售出后可使总的获利不少于780元，问有几种进货方案？如何进货？
【答案】(1) A型号每件50元,B型号每件60元;(2)三种方案;详见解析.
【解析】
(1)根据题意列出二元一次方程组解出即可；
(2)根据题意列出一元一次不等式组解出即可.
(1)设A型号每件x元,B型号每件y元.
由题意得：
解得：x=50，y=60，
答：A型号每件50元，B型号每件60元；
(2)设购进B型服装x件，则A型服装为（2x+4）件，
由题意得：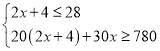
，
解得：10≤x≤12，
故进货方案有三种：①A型服装24件，B型服装10件；②A型服装26件，B型服装11件；③A型服装28件，B型服装12件；
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
相关题目
