题目内容
已知:如图,矩形ABCD的边BC在x轴上,E是对角线AC、BD的交点,反比例函数y=| 2 | x |
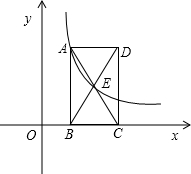 过A,E两点,点E的纵坐标为m.
过A,E两点,点E的纵坐标为m.(1)求点A坐标(用m表示)
(2)是否存在实数m,使四边形ABCD为正方形,若存在,请求出m的值;若不存在,请说明理由.
分析:(1)过E作EF⊥BC于F,由三角形中位线定理可得AB=2EF,即点A的纵坐标2m,进而可得可得A点坐标;
(2)设点E的坐标(
,m),由EF=BF得,m=
-
,解可得m的值.
(2)设点E的坐标(
| 2 |
| m |
| 2 |
| m |
| 1 |
| m |
解答: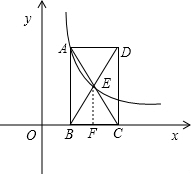 解:(1)过E作EF⊥BC于F,
解:(1)过E作EF⊥BC于F,
△ABC中,EF为其中位线,
由三角形中位线定理可得AB=2EF,
点A的纵坐标2m,
且点A在反比例函数y=
(x>0)上,
故A点坐标为(
,2m);
(2)根据题意,假设存在,且点E的坐标(
,m),
∵AB=BC=2m,中垂线BF=m,
∴EF=BF,m=
-
,
∴m2=1.
∴m=±1
m>0,
∴m=1.
 解:(1)过E作EF⊥BC于F,
解:(1)过E作EF⊥BC于F,△ABC中,EF为其中位线,
由三角形中位线定理可得AB=2EF,
点A的纵坐标2m,
且点A在反比例函数y=
| 2 |
| x |
故A点坐标为(
| 1 |
| m |
(2)根据题意,假设存在,且点E的坐标(
| 2 |
| m |
∵AB=BC=2m,中垂线BF=m,
∴EF=BF,m=
| 2 |
| m |
| 1 |
| m |
∴m2=1.
∴m=±1
m>0,
∴m=1.
点评:本题考查了反比例函数的图象的性质以及其与直线的关系,利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
相关题目
 已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF.
已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF. 19、已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE.
19、已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE. 上,AH=2,连接CF.
上,AH=2,连接CF. 已知:如图,矩形ABCD中,点E在边AB上,∠DEB的平分线EF交BC的延长线于点F,且AB=BF,连接DF.
已知:如图,矩形ABCD中,点E在边AB上,∠DEB的平分线EF交BC的延长线于点F,且AB=BF,连接DF. (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.