ƒøƒ⁄»ð
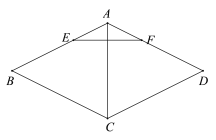
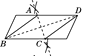
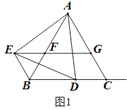
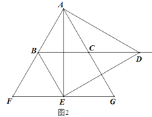
°æƒø°ø—ßœ∞¡À»˝Ω«∫Ø ˝∫Û£¨ ˝—ß—ßœ∞–°◊È∑¢œ÷£¨‘⁄µ»—¸»˝Ω«–Œ÷–“≤ø…“‘¿ýÀ∆µƒΩ®¡¢±þΩ«÷ƺ‰µƒ¡™œµ£Æ”⁄ «∂®“£∫µ»—¸»˝Ω«–Œ÷–µ◊±þ”Η¸µƒ±»Ω–◊ˆ∂•Ω«µƒ’˝∂‘£®sad£©£Æ“ª∏ˆΩ«µƒ¥Û–°”Î’‚∏ˆΩ«µƒ’˝∂‘÷µ“≤ «œýª•Œ®“ª»∑∂®µƒ£Æ»ÁÕº¢Ÿ‘⁄°˜ABC÷–£¨AB£ΩAC£¨∂•Ω«Aµƒ’˝∂‘º«◊˜sadA£Ω![]() £¨∏˘æð…œ ˆ∂®“£¨»ÁÕº¢⁄£¨Rt°˜ABC÷–£¨µ±sinA£Ω
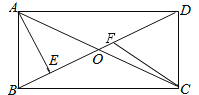
£¨∏˘æð…œ ˆ∂®“£¨»ÁÕº¢⁄£¨Rt°˜ABC÷–£¨µ±sinA£Ω![]() ±£¨‘ÚsadAµƒ÷µ «_____£Æ
±£¨‘ÚsadAµƒ÷µ «_____£Æ
°æ¥∞∏°ø![]()
°æΩ‚Œˆ°ø
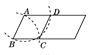
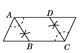
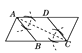
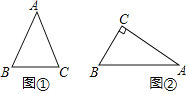
—”≥§ACµΩD£¨ πAD£ΩAB£¨‘⁄Rt°˜ACB÷–…ËBC£Ω3£¨«Û≥ˆAC£¨CDµƒ÷µ£¨‘Ÿ¿˚”√π¥π…∂®¿Ì«Û≥ˆBDº¥ø…Ω‚¥
Ω‚£∫—”≥§ACµΩD£¨ πAD£ΩAB£¨
‘⁄Rt°˜ACB÷–£¨sinA£Ω![]() £¨
£¨
…ËBC£Ω3£¨‘Ú”–AB£Ω5£¨AC£Ω![]() £Ω4£¨
£Ω4£¨
°ýAD£ΩAB£Ω5£¨CD£ΩAD©ÅAC£Ω5©Å4£Ω1£¨
‘⁄Rt°˜BCD÷–£¨CD£Ω1£¨BC£Ω3£¨
°ýBD£Ω![]() £¨
£¨
‘ÚsadA£Ω![]() £¨
£¨
π ¥∞∏Œ™£∫![]()


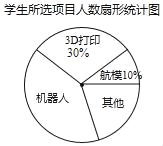
°æƒø°ø≥ı“ª£®1£©∞ý’Î∂‘°∞ƒ„◊Óœ≤∞ƵƒøŒÕ‚ªÓ∂؜Ӄø°±∂‘»´∞ý—ß…˙Ω¯––µ˜≤È£®√ø√˚—ß…˙∑÷±—°“ª∏ˆªÓ∂؜Ӄø£©£¨≤¢∏˘æðµ˜≤ÈΩ·π˚¡–≥ˆÕ≥º∆±Ì£¨ªÊ÷∆≥……»–ŒÕ≥º∆Õº£Æ
ƒ–°¢≈Æ…˙À˘—°œÓƒø»À ˝Õ≥º∆±Ì
œÓƒø | ƒ–…˙£®»À ˝£© | ≈Æ…˙£®»À ˝£© |
ª˙∆˜»À | 7 | 9 |
3D¥Ú”° | m | 4 |
∫Ωƒ£ | 2 | 2 |
∆‰À˚ | 5 | n |
∏˘æð“‘…œ–≈œ¢Ω‚戜¬¡–Œ £∫
£®1£©m=_____£¨n=_____£ª
£®2£©…»–ŒÕ≥º∆Õº÷–ª˙∆˜»ÀœÓƒøÀ˘∂‘”¶…»–Œµƒ‘≤–ƒΩ«∂» ˝Œ™_____°„£ª
£®3£©¥”—°∫Ωƒ£œÓƒøµƒ4√˚—ß…˙÷–Àʪ˙—°»°2√˚—ß…˙≤Œº”—ß–£∫Ωƒ£–À»§–°◊È—µ¡∑£¨«Î”√¡–æŸ∑®£®ª≠ ˜◊¥ÕºªÚ¡–±Ì£©«ÛÀ˘—°»°µƒ2√˚—ß…˙÷–«°∫√”–1√˚ƒ–…˙°¢1√˚≈Æ…˙µƒ∏≈¬ £Æ