题目内容
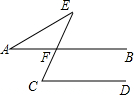如图，在AB∥CD，∠A=40°，∠C=80°．求∠E的度数．
解：∵AB∥CD，
∴∠EFB=∠C=80°，
而∠EFB=∠A+∠E，
∴∠E=∠EFB-∠A=80°-40°=40°．
分析：根据两直线平行，同位角相等得∠EFB=∠C=80°，再根据三角形外角的性质得到∠E=∠EFB-∠A，然后代值计算即可．
点评：本题考查了平行线的性质：两直线平行，同位角相等．也考查了三角形外角的性质．
∴∠EFB=∠C=80°，
而∠EFB=∠A+∠E，
∴∠E=∠EFB-∠A=80°-40°=40°．
分析：根据两直线平行，同位角相等得∠EFB=∠C=80°，再根据三角形外角的性质得到∠E=∠EFB-∠A，然后代值计算即可．
点评：本题考查了平行线的性质：两直线平行，同位角相等．也考查了三角形外角的性质．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
16、如图，在AB、AC上各取一点D、E，使得AE=AD，连接CD、BE相交于点O，再连接AO．若∠CAO=∠BAO，则图中全等三角形共有（ ）
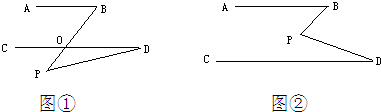
18、如图，在AB∥CD，∠A=40°，∠C=80°．求∠E的度数．