题目内容
【题目】如图，在平面直角坐标系网格中，将△ABC进行位似变换得到△A1B1C1．
（1）△A1B1C1与△ABC的位似比是______．
（2）画出△A1B1C1关于y轴对称的△A2B2C2．
（3）若点B的坐标为（3，1）为△ABC内一点，则依上述两次变换后，点B2的坐标是______．
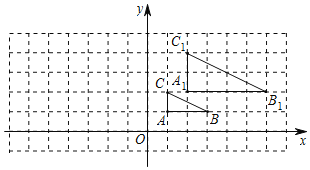
【答案】（1）1：2；（2）见解析；（3）（-6，2）
【解析】
（1）直接利用相似比得出答案；（2）利用轴对称图形的性质得出对应点位置即可；
（3）利用所画图形得出对应点坐标即可．
（1）△A1B1C1与△ABC的位似比是：1：2；
故答案为：1：2；
（2）如图所示：△A2B2C2，即为所求；
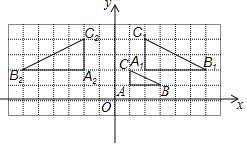
（3）点B2的坐标是：（-6，2）．
故答案为：（-6，2）．
练习册系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
【题目】已知二次函数y=ax2-4x+c，函数值y与自变量x之间的部分对应值如表：
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 15 | m | n | 0 | k | … |
（1）求这个二次函数的关系式．
（2）直接写出m、n、k之间的大小关系．（用“＞”连接）
（3）若点P在这个二次函数的图象上，且点P到x轴的距离为1，求点P的坐标．
