题目内容
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线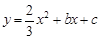 经过B点,且顶点在直线
经过B点,且顶点在直线 上.
上.
【小题1】求抛物线对应的函数关系式;
【小题2】若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由
【小题3】在(2)的条件下,连结BD,已知在对称轴上存在一点P,使得△PBD的周长最小.请求出点P的坐标.
【小题4】在(2)、(3)的条件下,若点M是线段OB上的一个动点(与点O、B不重合),过点M作MN∥BD交x轴于点N,连结PM、PN,设OM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在最大值?若存在,求出最大值并求此时M点的坐标;若不存在,请说明理由.
【小题1】∵抛物线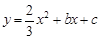 经过B(0,4),∴
经过B(0,4),∴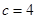 ,------1分
,------1分
∵顶点在直线 上,∴
上,∴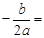
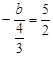 ,
, ,
,
∴所求函数关系式为: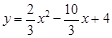 --------------------------------------2分
--------------------------------------2分
【小题2】在Rt△ABO中,OA=3,OB=4,∴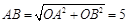 ,
,
∵四边形ABCD是菱形,∴BC=CD=DA=AB=5,
∴C、D两点的坐标分别是(5,4)、(2,0).---------------------------------3分
当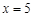 时,
时,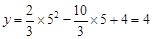 ,-----------------------------------------4分
,-----------------------------------------4分
当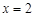 时,
时,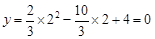 ,
,
∴点C和点D在所求抛物线上.--------------------------------------------------5分
【小题3】设CD与对称轴交于点P,则P为所求的点, --------------------------6分
设直线CD对应的函数关系式为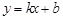 ,
,
则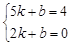 ,解得:
,解得: ,
,
∴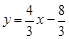 ,---------------------7分
,---------------------7分
当 时,
时,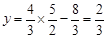 ,∴P(
,∴P(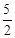 ,
,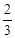 ),-------------------8分
),-------------------8分
【小题4】∵MN∥BD,∴△OMN∽△OBD,
∴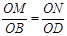 ,
, ,
,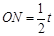 ,---------------9分
,---------------9分
设对称轴交x轴于点F,则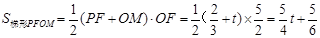 ,
,
∵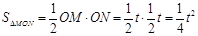 ,
,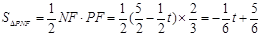 ,
,
∴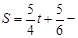
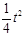
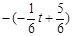
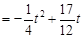 (
( -------------10分
-------------10分
由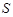
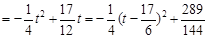 ,
,
∴当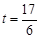 时,S取得最大值为
时,S取得最大值为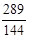 ,-----------------11分
,-----------------11分
此时点M的坐标为(0,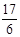 ).
).
解析

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案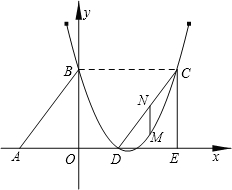 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y= 象在第四象限的交点,AB⊥x轴于B,且S△ABO=
象在第四象限的交点,AB⊥x轴于B,且S△ABO= 标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y= 如图,Rt△ABO的顶点A是反比例函数y=
如图,Rt△ABO的顶点A是反比例函数y=