题目内容
若直角三角形的两条直角边长为a,b,斜边长为c,斜边上的高为h,则以下列各组中三条线段为边长:①
,
,
;②
,
,
;③a,b,
h;④
,
,
.其中一定能组成直角三角形的是( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| h |
| a |
| b |
| c |
| 2 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| A、① | B、①③ | C、②③ | D、①②③④ |
分析:根据勾股定理的逆定理进行逐项分析解答即可.
解答:解:①由a2+b2=c2,ab=ch,推出c=
,所以
=h2,所以,
=
+
,故本项可以组成直角三角形;
②因为(
)2=a,(
)2=b,(
)2=c,由a、b、c组成三角形可知,a+b≠c,所以,本项不成组成直角三角形;
③因为,a2+b2=c2,(
h)2=2h2,但c2≠2h2,所以本项不能组成直角三角形;
④由(
)2=
,(
)2=
,(
)2=
,由①可知
+
≠
,所以本项不能组成直角三角形.
所以只有①项可以组成直角三角形.
故选择A.
| a2+b2 |
| a2b2 |
| a2+b2 |
| 1 |
| h2 |
| 1 |
| a2 |
| 1 |
| b2 |
②因为(
| a |
| b |
| c |
③因为,a2+b2=c2,(
| 2 |
④由(
| 1 | ||
|
| 1 |
| a |
| 1 | ||
|
| 1 |
| b |
| 1 | ||
|
| 1 |
| h |
| 1 |
| a |
| 1 |
| b |
| 1 |
| h |
所以只有①项可以组成直角三角形.
故选择A.
点评:本题主要考查直角三角形的逆定理,关键在于根据已知条件逐项进行分析解答.

练习册系列答案
相关题目
下列说法正确的是( )
A.若  ,且 ,且 的两条直角边分别是水平和竖直状态,那么 的两条直角边分别是水平和竖直状态,那么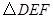 的两条直角边也一定分别是水平和竖直状态 的两条直角边也一定分别是水平和竖直状态 |
B.如果 , , ,那么 ,那么 |
| C.有一条公共边,而且公共边在每个三角形中都是腰的两个等腰三角形一定全等 |
| D.有一条相等的边,而且相等的边在每个三角形中都是底边的两个等腰三角形全等 |

 ,且
,且 的两条直角边分别是水平和竖直状态,那么
的两条直角边分别是水平和竖直状态,那么 的两条直角边也一定分别是水平和竖直状态
的两条直角边也一定分别是水平和竖直状态 ,
, ,那么
,那么