Question

【题目】等边三角形的内切圆半径、外接圆半径和高的比为(　　)

A. 1∶∶ B. 1∶2∶ C. 1∶∶2 D. 1∶2∶3

Answer 1

【答案】D

【解析】

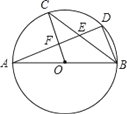
根据题意画图如下，作出辅助线OD、OE，证明△AOD为直角三角形且∠OAD为30°，即可求出OD、OA的比，进而求出内切圆半径、外接圆半径和高的比．

如图，连接OD、OE；

因为AB、AC切圆O与E.D，

所以OE⊥AB，OD⊥AC，

又因为AO=AO，

EO=DO，

所以△AEO≌△ADO(HL)，

故∠DAO=∠EAO；

又∵△ABC为等边三角形，

∴∠BAC=60，

∴∠OAC=60×=30，

∴OD:AO=1:2.

∵OF=OD，

所以OD:AF=1:（2+1）=1:3，

所以内切圆半径、外接圆半径和高的比是1:2:3.

故选D.