Question

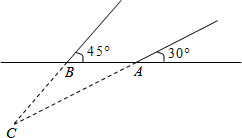（2013•娄底）2013年3月，某煤矿发生瓦斯爆炸，该地救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象．已知A、B两点相距4米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C的深度．（精确到0.1米，参考数据：

2

≈1.41，

3

≈1.73）

Answer 1

分析：过点C作CD⊥AB于点D，设CD=x，在Rt△ACD中表示出AD，在Rt△BCD中表示出BD，再由AB=4米，即可得出关于x的方程，解出即可．

解答：解：过点C作CD⊥AB于点D，
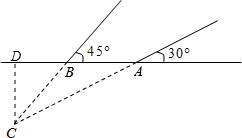设CD=x，
在Rt△ACD中，∠CAD=30°，
则AD=CD•cot30°=

3

CD=

3

x，
在Rt△BCD中，∠CBD=45°，
则BD=CD=x，
由题意得，

3

x-x=4，
解得：x=

4

3 -1

=2（

3

+1）≈5.5．
答：生命所在点C的深度为5.5米．

点评：本题考查了解直角三角形的应用，解答本题的关键是构造直角三角形，利用三角函数知识表示出相关线段的长度，注意方程思想的运用．