题目内容
已知∠AOB=120°,OC、OD是过点O的射线,射线OM、ON分别平分∠ACO和∠DOB.
(1)如图①,若OC、OD是∠AOB的三等分线,则∠MON
(2)如图②,若∠COD=40°,∠AOC≠∠DOB,则∠MON
(3)如图③,在∠AOB内,若∠COD=a(0°<a<60°),则∠MON
(4)将(3)中的∠COD绕着点O逆时针旋转到∠AOB的外部(0°<∠AOC<180°,0°<∠BOD<180°),求此时∠MON的度数.
(1)如图①,若OC、OD是∠AOB的三等分线,则∠MON
80
80
°(2)如图②,若∠COD=40°,∠AOC≠∠DOB,则∠MON
80
80
°(3)如图③,在∠AOB内,若∠COD=a(0°<a<60°),则∠MON
(60+
α)
| 1 |
| 2 |
(60+
α)
°| 1 |
| 2 |
(4)将(3)中的∠COD绕着点O逆时针旋转到∠AOB的外部(0°<∠AOC<180°,0°<∠BOD<180°),求此时∠MON的度数.

分析:(1)根据角平分线的定义得到∠AOC=∠COD=∠DOB=
×120°=40°,∠MOC=
∠AOC=20°,∠DON=
∠DOB=20°,则∠MON=20°+40°+20°=80°;
(2)根据角平分线的定义得到∠MOC=
∠AOC,∠DON=
∠DOB,而∠AOC+∠DOB=120°-40°=80°,则∠MOC+∠DON=40°,所以∠MON=40°+40°=80°;】
(3)与(2)一样得到∠AOC+∠DOB=120°-α,∠MOC+∠DON=60°-
α,则∠MON=60°-
α+α=60°+
α;
(4)反向延长OA、OB得到OA′、OB′,然后分类讨论:当OD、OC在∠AOB′内部;当OD、OC在∠A′OB′内部,可计算得到∠MON=120°-
α;
当OD、OC在∠A′OB内部,可计算得到∠MON=60°+
α;当OD、OC在∠A′OB′内部,可计算得到∠MON=120°-
α.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据角平分线的定义得到∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)与(2)一样得到∠AOC+∠DOB=120°-α,∠MOC+∠DON=60°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(4)反向延长OA、OB得到OA′、OB′,然后分类讨论:当OD、OC在∠AOB′内部;当OD、OC在∠A′OB′内部,可计算得到∠MON=120°-
| 1 |
| 2 |
当OD、OC在∠A′OB内部,可计算得到∠MON=60°+
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵OC、OD是∠AOB的三等分线,
∴∠AOC=∠COD=∠DOB=
×120°=40°,
∵射线OM、ON分别平分∠ACO和∠DOB,
∴∠MOC=
∠AOC=20°,∠DON=
∠DOB=20°,
∴∠MON=20°+40°+20°=80°;
(2)∵射线OM、ON分别平分∠ACO和∠DOB,
∴∠MOC=
∠AOC,∠DON=
∠DOB,
∴∠MOC+∠DON=
(∠AOC+∠DOB),
∵∠AOB=120°,∠COD=40°,
∴∠AOC+∠DOB=120°-40°=80°
∴∠MOC+∠DON=40°,
∴∠MON=40°+40°=80°;
(3)∵射线OM、ON分别平分∠AOC和∠DOB,
∴∠MOC=
∠AOC,∠DON=
∠DOB,
∴∠MOC+∠DON=
(∠AOC+∠DOB),
∵∠AOB=120°,∠COD=α,
∴∠AOC+∠DOB=120°-α,
∴∠MOC+∠DON=60°-
α,
∴∠MON=60°-
α+α=60°+
α;
故答案为80;80;(60+
α);
(4)反向延长OA、OB得到OA′、OB′,如图,
当OD、OC在∠AOB′内部,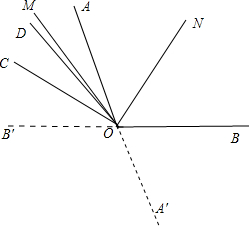 ,
,
设∠AOD=x,则∠AOC=α+x,
∴∠MOC=
∠AOC=
(α+x),∠DON=
∠DOB=60°+
x,
∴∠MON=∠BOC-∠COD-∠BON=120°+α+x-
(x+α)-(60°-
x)=60°+
α;
当OD、OC在∠A′OB′内部,可计算得到∠MON=120°-
α;
当OD、OC在∠A′OB内部,可计算得到∠MON=60°+
α;
当OD、OC在∠A′OB′内部,可计算得到∠MON=120°-
α.
∴∠AOC=∠COD=∠DOB=
| 1 |
| 3 |
∵射线OM、ON分别平分∠ACO和∠DOB,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=20°+40°+20°=80°;
(2)∵射线OM、ON分别平分∠ACO和∠DOB,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MOC+∠DON=
| 1 |
| 2 |
∵∠AOB=120°,∠COD=40°,
∴∠AOC+∠DOB=120°-40°=80°
∴∠MOC+∠DON=40°,
∴∠MON=40°+40°=80°;
(3)∵射线OM、ON分别平分∠AOC和∠DOB,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MOC+∠DON=
| 1 |
| 2 |
∵∠AOB=120°,∠COD=α,
∴∠AOC+∠DOB=120°-α,
∴∠MOC+∠DON=60°-
| 1 |
| 2 |
∴∠MON=60°-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为80;80;(60+
| 1 |
| 2 |
(4)反向延长OA、OB得到OA′、OB′,如图,
当OD、OC在∠AOB′内部,
 ,
,设∠AOD=x,则∠AOC=α+x,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠BOC-∠COD-∠BON=120°+α+x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当OD、OC在∠A′OB′内部,可计算得到∠MON=120°-
| 1 |
| 2 |
当OD、OC在∠A′OB内部,可计算得到∠MON=60°+
| 1 |
| 2 |
当OD、OC在∠A′OB′内部,可计算得到∠MON=120°-
| 1 |
| 2 |
点评:本题考查了角度的计算:1直角为90°,1平角为180°.也考查了角平分线的性质.

练习册系列答案
相关题目

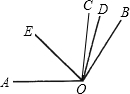 如图所示,已知∠AOB=120°,∠AOC是直角,OD平分∠BOC,OE平分∠AOC,求∠DOE的度数.
如图所示,已知∠AOB=120°,∠AOC是直角,OD平分∠BOC,OE平分∠AOC,求∠DOE的度数. 如图,已知∠AOB=120°,∠COD是∠AOB内的一个角,OE是∠AOC的平分线,OF是∠BOD的平分线.
如图,已知∠AOB=120°,∠COD是∠AOB内的一个角,OE是∠AOC的平分线,OF是∠BOD的平分线.