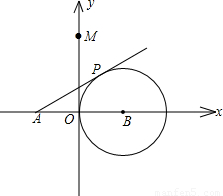题目内容
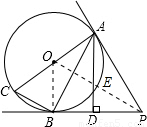
(2008•潍坊)如图,AC是圆O的直径,AC=10厘米,PA,PB是圆O的切线,A,B为切点,过A作AD⊥BP,交BP于D点,连接AB,BC.(1)求证:△ABC∽△ADB;
(2)若切线AP的长为12厘米,求弦AB的长.
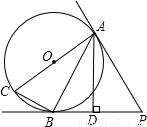
【答案】分析:(1)根据AC为⊙O的半径,可知:∠ABC=90°,由AD⊥BP,可知:∠ABC=∠ADB,根据切线的性质知:∠ABD=∠ACB,从而可证:△ABC∽△ADB;
(2)在Rt△POA中,根据勾股定理可将OP的长求出,再根据△ABC∽△PAO,可将AB的长求出.
解答: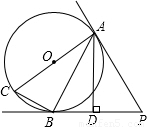 (1)证明:∵AC是圆O的直径,
(1)证明:∵AC是圆O的直径,
∴∠ABC=90°,
∵AD⊥BP,
∴∠ADB=90°,
∴∠ABC=∠ADB,
∵PA是圆O的切线,
∴∠PAB=∠ACB,
又∵PA=PB,
∴∠PAB=∠ABD,
∴∠ABD=∠ACB,
[也可以为:∵PA,PB是圆O的切线,
∴∠ABD=∠ACB(弦切角定理)]
在△ABC和△ADB中:
∵∠ABC=∠ADB,∠ABD=∠ACB,
∴△ABC∽△ADB;
(2)解:连接OP,OB,
∵PA是⊙O的切线,AC是⊙O的直径,
∴∠ABC=∠OAP,
在Rt△AOP中,AP=12厘米,OA=5厘米
∴OP=13厘米
∵PA、PB是⊙O的切线,
∴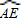 =
= ,
,
∴∠AOE= ∠AOB=∠ACB,
∠AOB=∠ACB,
在△ABC与△PAO中,
∵∠AOE=∠ACB,∠ABC=∠OAP,
∴△ABC∽△PAO,
∴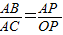 ,
,
∴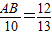 ,
,
∴AB= 厘米.
厘米.
点评:本题主要考查相似三角形的判定及切线性质的应用.
(2)在Rt△POA中,根据勾股定理可将OP的长求出,再根据△ABC∽△PAO,可将AB的长求出.
解答:
 (1)证明:∵AC是圆O的直径,
(1)证明:∵AC是圆O的直径,∴∠ABC=90°,
∵AD⊥BP,
∴∠ADB=90°,
∴∠ABC=∠ADB,
∵PA是圆O的切线,
∴∠PAB=∠ACB,
又∵PA=PB,
∴∠PAB=∠ABD,
∴∠ABD=∠ACB,
[也可以为:∵PA,PB是圆O的切线,
∴∠ABD=∠ACB(弦切角定理)]
在△ABC和△ADB中:
∵∠ABC=∠ADB,∠ABD=∠ACB,
∴△ABC∽△ADB;
(2)解:连接OP,OB,
∵PA是⊙O的切线,AC是⊙O的直径,
∴∠ABC=∠OAP,
在Rt△AOP中,AP=12厘米,OA=5厘米
∴OP=13厘米
∵PA、PB是⊙O的切线,
∴
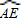 =
= ,
,
∴∠AOE=
 ∠AOB=∠ACB,
∠AOB=∠ACB,在△ABC与△PAO中,
∵∠AOE=∠ACB,∠ABC=∠OAP,
∴△ABC∽△PAO,
∴
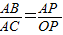 ,
,∴
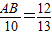 ,
,∴AB=
 厘米.
厘米.点评:本题主要考查相似三角形的判定及切线性质的应用.

练习册系列答案
相关题目
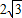 ,0)作圆B的切线交圆于点P,已知tan∠PAB=
,0)作圆B的切线交圆于点P,已知tan∠PAB=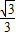 ,抛物线C经过A,P两点.
,抛物线C经过A,P两点.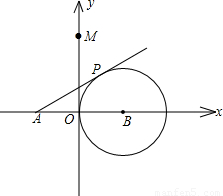
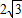 ,0)作圆B的切线交圆于点P,已知tan∠PAB=
,0)作圆B的切线交圆于点P,已知tan∠PAB=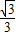 ,抛物线C经过A,P两点.
,抛物线C经过A,P两点.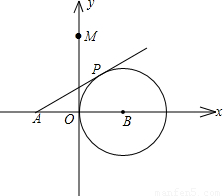
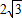 ,0)作圆B的切线交圆于点P,已知tan∠PAB=
,0)作圆B的切线交圆于点P,已知tan∠PAB=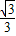 ,抛物线C经过A,P两点.
,抛物线C经过A,P两点.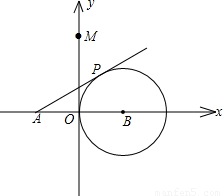
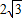 ,0)作圆B的切线交圆于点P,已知tan∠PAB=
,0)作圆B的切线交圆于点P,已知tan∠PAB=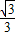 ,抛物线C经过A,P两点.
,抛物线C经过A,P两点.