题目内容
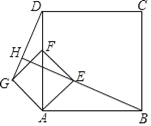
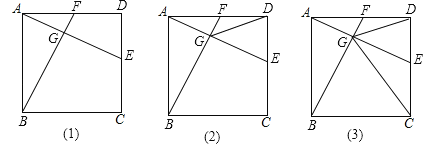
【题目】如图(1)在正方形ABCD中,点E是CD边上一动点,连接AE,作BF⊥AE,垂足为G交AD于F
(1)求证:AF=DE;
(2)连接DG,若DG平分∠EGF,如图(2),求证:点E是CD中点;
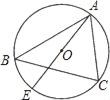
(3)在(2)的条件下,连接CG,如图(3),求证:CG=CD.
【答案】(1)见解析;(2)见解析;(3)CG=CD,见解析.
【解析】
(1)证明△BAF≌△ADE(ASA)即可解决问题.
(2)过点D作DM⊥GF,DN⊥GE,垂足分别为点M,N.想办法证明AF=DF,即可解决问题.
(3)延长AE,BC交于点P,由(2)知DE=CD,利用直角三角形斜边中线的性质,只要证明BC=CP即可.
(1)证明:如图1中,
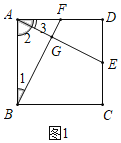
在正方形ABCD中,AB=AD,∠BAD=∠D=90o,
∴∠2+∠3=90°
又∵BF⊥AE,
∴∠AGB=90°
∴∠1+∠2=90°,
∴∠1=∠3
在△BAF与△ADE中,
∠1=∠3 BA=AD ∠BAF=∠D,
∴△BAF≌△ADE(ASA)
∴AF=DE.
(2)证明:过点D作DM⊥GF,DN⊥GE,垂足分别为点M,N.
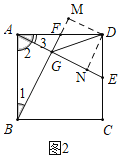
由(1)得∠1=∠3,∠BGA=∠AND=90°,AB=AD
∴△BAG≌△ADN(AAS)
∴AG=DN,
又DG平分∠EGF,DM⊥GF,DN⊥GE,
∴DM=DN,
∴DM=AG,又∠AFG=∠DFM,∠AGF=∠DMF
∴△AFG≌△DFM(AAS),
∴AF=DF=DE=![]() AD=
AD=![]() CD,
CD,
即点E是CD的中点.
(3)延长AE,BC交于点P,由(2)知DE=CD,
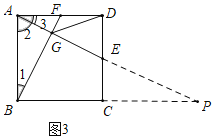
∠ADE=∠ECP=90°,∠DEA=∠CEP,
∴△ADE≌△PCE(ASA)
∴AE=PE,
又CE∥AB,
∴BC=PC,
在Rt△BGP中,∵BC=PC,
∴CG=![]() BP=BC,
BP=BC,
∴CG=CD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目