��Ŀ����
����Ŀ�� ��ͼ,Rt��ABC ��,��ACB=90 ,AC=6cm,BC=8cm,���� P �ӵ� B ����,�� BA������ÿ�� 5cm ���ٶ���� A �����˶�,ͬʱ���� Q �ӵ� C ����,�� CB ������ÿ�� 4cm �� �ٶ���� B �����˶�,�˶�ʱ��Ϊ t ��(0<t<2)������ PQ.
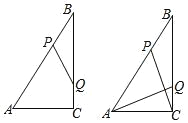
(1)����BPQ ���ABC ���ƣ��� t ��ֵ��
(2)�� t Ϊ��ֵʱ���ı��� ACQP �������С����Сֵ�Ƕ���?
(3)���� AQ��CP���� AQ��CP���� t ��ֵ��
���𰸡�(1) ���� t=1 �� t=![]() ʱ����BPQ ����ABC ����;(2)18;(3) t=
ʱ����BPQ ����ABC ����;(2)18;(3) t=![]()
��������
����������BPQ����BAC �����ٽ�������б�ʽ�����ʣ����ı��� ACQP �����ʽ�ú�t�ı���ʽ��ʾ��������������Сֵ������ P �� PM��BC �ڵ� M���� AQ �� CP �ཻ�ڵ� N����֤����ACQ��CMP�������ý�����tֵ.
(1)�١�BPQ����BAC ����ʱ����![]()
��BP=5t��QC=4t��AC=6cm��BC=8cm��
��![]() ����ã�t=1��
����ã�t=1��
����BPQ����BCA ����ʱ��
��![]() ,��
,��![]() ����ã�t=
����ã�t=![]()
�ۺ��������� t=1 �� t=![]() ʱ����BPQ ����ABC ���ƣ�
ʱ����BPQ ����ABC ���ƣ�
(2)�� PM��BC �ڵ� M.����BPM����BAC��
��![]() ,��
,��![]() ����ã�PM=3t��
����ã�PM=3t��
���ı��� ACQP �����Ϊ y,������ã�y=![]() ��6��8
��6��8![]() (84t)��3t=6(t1)2+18
(84t)��3t=6(t1)2+18
�൱ t=1 ʱ�������СΪ 18.
(3)���� P �� PM��BC �ڵ� M���� AQ �� CP �ཻ�ڵ� N������ PB=3t��MC=84t��
�ߡ�NAC+��NCA=90 ,��PCM+��NCA=90 �����NAC=��PCM�� �֡ߡ�ACQ=��CMP=90 �����ACQ��CMP��
��![]() ,��
,��![]() ����ã�t=
����ã�t=![]()

 ��У����ϵ�д�
��У����ϵ�д�