题目内容
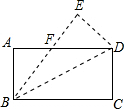如图，一块矩形纸片ABCD，长BC=8cm，宽CD=6cm，将这块矩形纸片沿对角线BD对折（折痕与折叠后得到的图形用虚线表示），得到△BDE，则EF=| 7 |
| 4 |
| 7 |
| 4 |
分析：首先证明FD=BF，再设EF=xcm，则BF=FD=（8-x）cm，再在Rt△EFD中利用勾股定理逆定理62+x2=（8-x）2，解出x的值即可．
解答：
解：根据折叠可得∠1=∠2，DE=CD=6cm，
∵AD∥BC，
∴∠1=∠3，
∴∠2=∠3，
∴FD=BF，
设EF=xcm，则BF=FD=（8-x）cm，
在Rt△EFD中：ED2+EF2=FD2，
62+x2=（8-x）2，
解得：x=
，
即EF=
，
故答案为：
．
解：根据折叠可得∠1=∠2，DE=CD=6cm，∵AD∥BC，
∴∠1=∠3，
∴∠2=∠3，
∴FD=BF，
设EF=xcm，则BF=FD=（8-x）cm，
在Rt△EFD中：ED2+EF2=FD2，
62+x2=（8-x）2，
解得：x=
| 7 |
| 4 |
即EF=
| 7 |
| 4 |
故答案为：
| 7 |
| 4 |
点评：此题主要考查了图形的翻折变换，以及勾股定理的应用，关键是要理解折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，只是位置变化．
练习册系列答案
相关题目
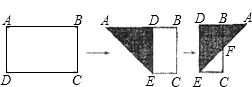
如图，一块矩形纸片ABCD，长BC=8cm，宽CD=6cm，将这块矩形纸片沿对角线BD对折（折痕与折叠后得到的图形用虚线表示），得到△BDE，则EF=________．
C．
D．