题目内容
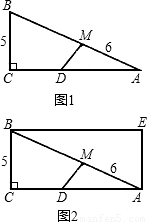
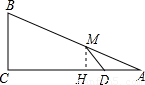
如图1,Rt△ABC中,∠C=90°,AC=12,BC=5,点M在边AB上,且AM=6.(1)动点D在边AC上运动,且与点A,C均不重合,设CD=x.
①设△ABC与△ADM的面积之比为y,求y与x之间的函数关系式(写出自变量的取值范围);
②当x取何值时,△ADM是等腰三角形?写出你的理由.
(2)如图2,以图1中的为一组邻边的矩形中,动点在矩形边上运动一周,能使是M为顶角的等腰三角形共有多少个?(直接写结果,不要求说明理由)
【答案】分析:(1)△ABC的面积易求,△ADM的面积应利用相似比表示出AD及AD边上的高,然后求出面积比值,△ADM是等腰三角形,两腰是不确定的,所以应分AM=DM,AM=AD,DM=AD来分别讨论;
(2)M为顶角,那么AM=DM,只需作出M为圆心,MA=6为半径的圆,看与矩形有几个交点即可.
解答: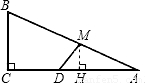 解:(1)①∵Rt△ABC中,∠C=90°,AC=12,BC=5,
解:(1)①∵Rt△ABC中,∠C=90°,AC=12,BC=5,
∴S△ABC=30,AB=13,
过M作MH⊥AC于H,则MH∥BC,
∴ ,
,
∴MH=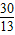 ,
,
∵CD=x,
∴AD=12-x,
∴S△ADM= (12-x),
(12-x),
∴y=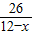 (0<x<12);
(0<x<12);
②(i)当AD=AM=6,即x=6时,△ADM为等腰三角形;
(ii)当AM=MD时,AD=2AH.
∴AH=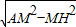 =
=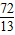 ,
,
∴AD=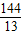 ,
,
即x=12-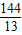 =
=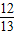 时,△ADM为等腰三角形;
时,△ADM为等腰三角形;
(iii)当AD=MD时,
∵AD=12-x,AH=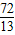 ,
,
∴HD=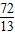 -(12-x)=x-
-(12-x)=x-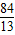 ,
,
∵MH2+HD2=MD2,
∴(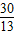 )2+(x-
)2+(x-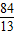 )2=(12-x)2,
)2=(12-x)2,
解得:x=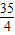 时,△ADM为等腰三角形.
时,△ADM为等腰三角形.
(2)4个.
(根据题意,以M为圆心,MA=6为半径作圆,与AC、AE、BE三边共有包括A点在内的5个交点,所以符合条件的等腰三角形共有4个)
点评:一个三角形是等腰三角形,可让其任意两条边相等分3种情况探讨;确定顶角的等腰三角形,相应的腰长也就确定,注意动手操作即可得到答案.
(2)M为顶角,那么AM=DM,只需作出M为圆心,MA=6为半径的圆,看与矩形有几个交点即可.
解答:
 解:(1)①∵Rt△ABC中,∠C=90°,AC=12,BC=5,
解:(1)①∵Rt△ABC中,∠C=90°,AC=12,BC=5,∴S△ABC=30,AB=13,
过M作MH⊥AC于H,则MH∥BC,
∴
 ,
,∴MH=
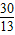 ,
,∵CD=x,
∴AD=12-x,
∴S△ADM=
 (12-x),
(12-x),∴y=
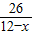 (0<x<12);
(0<x<12);②(i)当AD=AM=6,即x=6时,△ADM为等腰三角形;
(ii)当AM=MD时,AD=2AH.
∴AH=
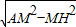 =
=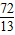 ,
,
∴AD=
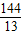 ,
,即x=12-
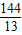 =
=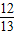 时,△ADM为等腰三角形;
时,△ADM为等腰三角形;(iii)当AD=MD时,
∵AD=12-x,AH=
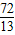 ,
,∴HD=
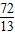 -(12-x)=x-
-(12-x)=x-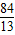 ,
,∵MH2+HD2=MD2,
∴(
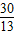 )2+(x-
)2+(x-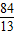 )2=(12-x)2,
)2=(12-x)2,解得:x=
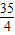 时,△ADM为等腰三角形.
时,△ADM为等腰三角形.(2)4个.
(根据题意,以M为圆心,MA=6为半径作圆,与AC、AE、BE三边共有包括A点在内的5个交点,所以符合条件的等腰三角形共有4个)
点评:一个三角形是等腰三角形,可让其任意两条边相等分3种情况探讨;确定顶角的等腰三角形,相应的腰长也就确定,注意动手操作即可得到答案.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 (2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
(2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论: (2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为
(2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=9cm,则AB的长为( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=9cm,则AB的长为( ) 的外接圆.
的外接圆. (2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.
(2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.