题目内容
已知，如图，在直角坐标系中O是坐标原点，四边形AOCB是矩形，0C=6，OA=2，P是边AB上的任意一点．当点P在边AB上移动时，是否存在这样的点P使得OP⊥PC成立？若存在，请求出点P的坐标，画出满足条件的P点，并求出经过D、P、C三点的抛物线的对称轴；若不存在这样的P点，请说明理由．
【答案】分析：本题要懂得数形结合．当点P位于A、B点时，结论不成立．但当P点在边AB上且与A、B点不重合时，连接OP、PC，若有OP⊥PC，则应有△AOP∽△BPC，再求出PA，然后求出OP⊥PC的P点坐标，最后证明抛物线是轴对称图形求出对称轴．
解答：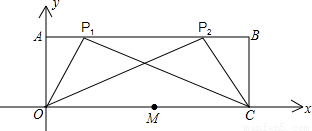
解：在边AB上存在这样的点P使得OP⊥PC成立．
显然当点P位于A、B点时，结论不成立．
当P点在边AB上且与A、B点不重合时，连接OP、PC，
若有OP⊥PC，
则应有△AOP∽△BPC，PA=3±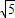
当P点分别位于P1（3-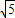
，2）和P2（3+
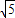，2）时，OP⊥PC成立．
以OC的中点M为圆心，半径长为3画圆与AB交于P1、P2点．
则点Pl、P2即为所要画的点已知抛物线的图象经过坐标原点和点C（6，O）
∵抛物线是轴对称图形
∴抛物线的对称轴是x=3．
点评：本题重点在于考生要懂得数形结合分析问题以及理解抛物线的性质，难度中等．
解答：
解：在边AB上存在这样的点P使得OP⊥PC成立．显然当点P位于A、B点时，结论不成立．
当P点在边AB上且与A、B点不重合时，连接OP、PC，
若有OP⊥PC，
则应有△AOP∽△BPC，PA=3±
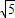
当P点分别位于P1（3-
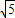，2）和P2（3+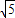，2）时，OP⊥PC成立．以OC的中点M为圆心，半径长为3画圆与AB交于P1、P2点．
则点Pl、P2即为所要画的点已知抛物线的图象经过坐标原点和点C（6，O）
∵抛物线是轴对称图形
∴抛物线的对称轴是x=3．
点评：本题重点在于考生要懂得数形结合分析问题以及理解抛物线的性质，难度中等．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
的图象的一个分支位于第一象限．
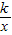的图象的图象上，求k的值；
S1？
的图象与y轴交于点A，
的图象分别交于点M，N，已知△AOB的面积为1，点M的纵坐
时x的取值范围。
中，四边形OABC是矩形，点A，C的坐
＝－
＋
交折线O－A－B于点E．
