题目内容
14、已知二次函数y=ax2+bx+c的图象经过(0,3),且开口向上.请写出符合要求的一个二次函数的解析式:
y=x2+3
.分析:根据二次函数的图象开口向上知道a>0,又二次函数的图象过(0,3),可以得到c=3,所以解析式满足a>0,c=3即可.
解答:解:∵抛物线y=ax2+bx+c的开口向上,且经过(0,3),
∴a>0,c=0,
满足条件的解析式不唯一,
如当a=1,b=0,c=3,即y=x2+3.
故答案为y=x2+3.
∴a>0,c=0,
满足条件的解析式不唯一,
如当a=1,b=0,c=3,即y=x2+3.
故答案为y=x2+3.
点评:本题主要考查二次函数的性质的知识点,此题是开放性试题,考查函数图形及性质的综合运用,对考查学生所学函数的深入理解、掌握程度具有积极的意义,但此题若想答对需要满足所有条件,如果学生没有注意某一个条件就容易错.本题的结论是不唯一的,其解答思路渗透了数形结合的数学思想.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
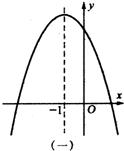 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
