Question

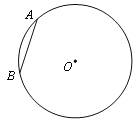
【题目】如图，在半径为2的⊙O中，弦AB＝2，⊙O上存在点C，若AC＝2，则∠BAC的度数为___.

Answer 1

【答案】30°或105°

【解析】

先根据条件证明△AOB为等边三角形，第一种情况，再证△AOC为等腰直角三角形，即可得解；第二种情况，直接用圆周角定理即可得解.

解：①如图，连接AO,过O作OD⊥AB于D, 作OE⊥AC于E,

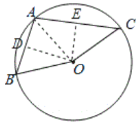
∵AB＝2，OA=OB=OC=2,

∴AB=OA=OB，

∴△ABO为等边三角形.

∴∠BAO=60°.

又∵AC=2，

∴ ，

∴△AOC为等腰直角三角形.

则∠OAC=45°，

∴∠BAC=105°.

②如图，

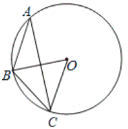
同上，△OBC为等边三角形.

∴∠O=60°，

∴∠BAC=30°.

综上，∠BAC的度数为30°或105°.