题目内容
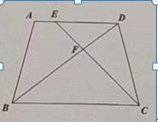
【题目】如图
在等腰梯形中，
，E为
上一点，且AE:DE=1:3，联结
和
，与交于点F，如果
，
。
（1）求梯形的周长
（2）求线段CF的长度
【答案】（1）
；（2）
.
【解析】
（1）过A做AM∥CD，交BC于M，先证明△ABM∽△BCD,解得AB的长度，从而利用梯形的周长公式求解即可
（2）先证明△EDF∽△BDA,求出EF的值，因为AD∥BC,利用平行线分线段成比例求解即可
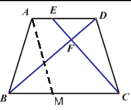
（1） 如图，过A做AM∥CD，交BC于M
∵AD∥BC，AM∥CD
∴四边形AMCD是平行四边形
∴AD=MC=4，AM=CD
∵梯形ABCD是等腰梯形
∴AB=CD
∴AB=AM
∴∠ABM=∠AMB
∵BD=BC=6
∴∠BDC=∠BCD
∵AM∥CD
∴∠AMB=∠BCD
∴△ABM∽△BCD
∴
∴BM=6-4=2
∴
∴AB=
∴CD=AB=
∴梯形ABCD周长=AB＋BC＋CD＋AD=10＋
（2）∵AE:DE=1:3,AD=4
∴DE=
∵AD∥BC
∴
∵BC=BD=6
∴
∴BF=2DF，CF=2EF
∴BD=3DF=6
∴DF=2
∴
=
∵∠EDF=∠BDA
∴△EDF∽△BDA
∴EF=AB=
∴CF=2EF=
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
相关题目
