��Ŀ����
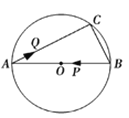
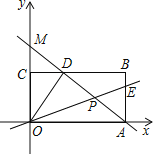
����Ŀ����ͼ����֪�����߾�����A��![]() ��0����B��4��0����C��0��2�����㣬��D���C����
��0����B��4��0����C��0��2�����㣬��D���C����![]() ��Գƣ���P��
��Գƣ���P��![]() ���ϵ�һ�����㣬���P������Ϊ��
���ϵ�һ�����㣬���P������Ϊ��![]() ��0��������P��
��0��������P��![]() ��Ĵ��߽��������ڵ�Q����ֱ��BD�ڵ�M��
��Ĵ��߽��������ڵ�Q����ֱ��BD�ڵ�M��
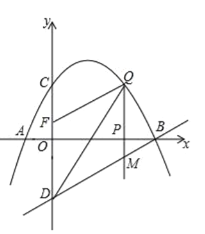
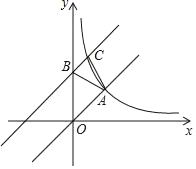
��1���������������ʾ�Ķ��κ����ı���ʽ��
��2����P���߶�AB���˶��Ĺ����У��Ƿ���ڵ�Q��ʹ����B��Q��MΪ��������������BOD���ƣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
��3����֪��F��0��![]() ������P��
������P��![]() �����˶�������
�����˶�������![]() Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
���𰸡���1��![]() ����2�����ڵ�Q��ʹ����B��Q��MΪ��������������BOD���ƣ���Q������Ϊ��3��2����
����2�����ڵ�Q��ʹ����B��Q��MΪ��������������BOD���ƣ���Q������Ϊ��3��2����![]() ��0������3����
��0������3����![]() ��
��![]() ��
��![]() ��
��![]() ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
��������
��1������������������ߵĽ���ʽΪ![]() ���ó�a��ֵ���ٴ������ʽ����
���ó�a��ֵ���ٴ������ʽ����
��2�����ڵ�Q��ʹ����B��Q��MΪ��������������BOD���ƣ����Ϊ������������ٵ���DOB=��MBQ=90��ʱ�����Եõ���MBQ�ס�BPQ���ɽ�𣬢ڵ���BQM=90��ʱ����ʱ��Q���A�غϣ���BOD�ס�BQM�伴�ɽ��
��3�����������֪��D����Ϊ��0��![]() �����õ�ֱ��BD����ʽΪ
�����õ�ֱ��BD����ʽΪ![]() ����ΪQM��
����ΪQM��![]() �ᣬP��
�ᣬP��![]() ��0������
��0������![]() ����ΪF
����ΪF![]() ��
��![]() ��D��0��
��D��0��![]() ����
����![]() �����Ե�QM=DF����
�����Ե�QM=DF����![]() ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ����ɽ��
ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ����ɽ��
�⣺��1���������߹���A��![]() ��0����B��4��0����
��0����B��4��0����
����������ߵĽ���ʽΪ![]() ��
��
�������߾�����C��0��2����
��![]() ��
��
��ã�![]() ��
��
�������߽���ʽΪ![]() ��
��
��2�����ڵ�Q��ʹ����B��Q��MΪ��������������BOD����.
��ͼ��ʾ��
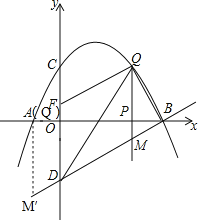
��QM��DC��
���ODB=��QMB��
���������������
�ٵ���DOB=��MBQ=90��ʱ����DOB�ס�MBQ��
��![]() ��
��
�ߡ�MBQ=90�㣬
���MBP+��PBQ=90�㣬
�ߡ�MPB=��BPQ=90�㣬
���MBP+��BMP=90�㣬
���BMP=��PBQ��
���MBQ�ס�BPQ��
��![]() ��
��
��P��![]() ��0����B��4��0����
��0����B��4��0����
��BP![]() ��
��![]() ��
��
�� ��
��
��ã�![]() ��
��
��![]() ʱ����P��Q��M�����B�غϣ����ܹ��������Σ���ȥ��
ʱ����P��Q��M�����B�غϣ����ܹ��������Σ���ȥ��
��![]() ����Q��������3��2���� ,
����Q��������3��2���� ,
�ڵ���BQM=90��ʱ����ʱ��Q���A�غϣ���BOD�ס�BQM�䣬
��ʱm=-1����Q������Ϊ��![]() ��0����
��0����
���ϣ���Q������Ϊ��3��2����![]() ��0��ʱ���Ե�B��Q��MΪ��������������BOD���ƣ�
��0��ʱ���Ե�B��Q��MΪ��������������BOD���ƣ�
��3���ߵ�D���C��0��2������![]() ��Գƣ�
��Գƣ�
���D������0��![]() ����
����
��ֱ��BD����ʽΪ![]() ��
��
���У�![]() ����ã�
����ã�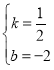 ��
��
��ֱ��BD����ʽΪ![]() ��
��
��QM��![]() �ᣬP��
�ᣬP��![]() ��0����
��0����
��Q![]() ��M
��M![]() ��
��
��![]() ��
��
��F![]() ��
��![]() ��D��0��
��D��0��![]() ����
����
��![]() ��
��
��QM��DF��
�൱QM=DF����![]() ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
��ã�m=-1��m=3��![]() ��
��![]() ��
��
��m=-1��m=3��![]() ��
��![]() ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�