题目内容
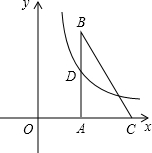 如图,Rt△ABC中,∠BAC=90°,BC所在直线的解析式为
如图,Rt△ABC中,∠BAC=90°,BC所在直线的解析式为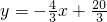 ,AC=3,若AB的中点D在双曲线
,AC=3,若AB的中点D在双曲线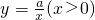 上,求a的值。
上,求a的值。
解:由BC的解析式可得点C为(5,0),又∵AC=3,
∴可得A(2,0),因为AB垂直于x轴,可得B的横坐标为2.
而B在直线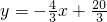 上,所以可得B点坐标为(2,4).
上,所以可得B点坐标为(2,4).
由A和B的坐标可得出D点坐标(2,2).
将D点坐标代入y= 可求出:a=4.
可求出:a=4.
分析:根据BC的解析式,AC=3,可得点C点坐标、A点坐标和B的横坐标,而B在直线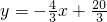 上,所以可得B点坐标,由A和B的坐标可得出D点坐标,将D点坐标代入双曲线可求出a值.
上,所以可得B点坐标,由A和B的坐标可得出D点坐标,将D点坐标代入双曲线可求出a值.
点评:本题考查了待定系数法求反比例函数解析式关键在于A点和B点坐标的求解及求出坐标后的运用,这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
∴可得A(2,0),因为AB垂直于x轴,可得B的横坐标为2.
而B在直线
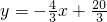 上,所以可得B点坐标为(2,4).
上,所以可得B点坐标为(2,4).由A和B的坐标可得出D点坐标(2,2).
将D点坐标代入y=
 可求出:a=4.
可求出:a=4.分析:根据BC的解析式,AC=3,可得点C点坐标、A点坐标和B的横坐标,而B在直线
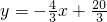 上,所以可得B点坐标,由A和B的坐标可得出D点坐标,将D点坐标代入双曲线可求出a值.
上,所以可得B点坐标,由A和B的坐标可得出D点坐标,将D点坐标代入双曲线可求出a值.点评:本题考查了待定系数法求反比例函数解析式关键在于A点和B点坐标的求解及求出坐标后的运用,这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.