题目内容
某校初一(1)班的同学要从10名候选人中投票选举班干部.如果每个同学必须投票且只能投票选举两候选人,若要保证必有两个及以上的同学投相同的两名候选人的票,那么这个班的同学至少应有( )
| A、10人 | B、11人 | C、45人 | D、46人 |
分析:首先根据组合求出10名任选2名的票数,那么这个班的同学最少人数就是票数+1.
解答:解:∵10名任选2名的组合共有
=
=45种
∵如果有45人参与投票,不能保证必有2人,因为可能恰好产生以上45种投票结果.
∵为保障必有2人投同样的票
∴至少有45+1=46人,
故选D.
| C | 2 10 |
| 10×9 |
| 2 |
∵如果有45人参与投票,不能保证必有2人,因为可能恰好产生以上45种投票结果.
∵为保障必有2人投同样的票
∴至少有45+1=46人,
故选D.
点评:本题考查抽屉原理.解决本题的关键是结合组合知识,求得投票数.

练习册系列答案
相关题目
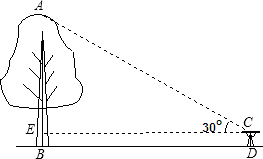 如图,我市某校初三(一)班的同学要测一棵树AB的高度.在离树24m的D处,用测角仪测得树顶A的仰角为30°,已知测角仪的高CD=1m,求树高AB(结果保留根号)
如图,我市某校初三(一)班的同学要测一棵树AB的高度.在离树24m的D处,用测角仪测得树顶A的仰角为30°,已知测角仪的高CD=1m,求树高AB(结果保留根号)