题目内容
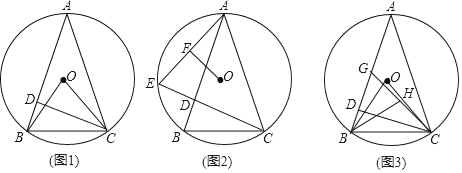
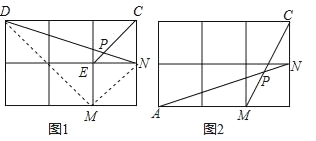
【题目】(问题呈现)如图1,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
(方法归纳)求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
(问题解决)(1)直接写出图1中tan∠CPN的值为 ;
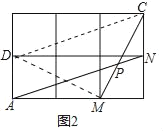
(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值.
【答案】(1)2;(2)![]()
【解析】
(1)结合已知可得tan∠CPN=tan∠DNM=![]() ;(2)取格点D,连接CD,DM.由∠DCM=∠D=45°得,cos∠CPN=cos∠DCM=
;(2)取格点D,连接CD,DM.由∠DCM=∠D=45°得,cos∠CPN=cos∠DCM=![]() .
.
解:(1)如图1中,
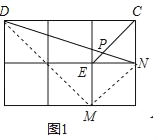
∵EC∥MN,
∴∠CPN=∠DNM,
∴tan∠CPN=tan∠DNM,
∵∠DMN=90°,
∴tan∠CPN=tan∠DNM=![]() =2;
=2;
(2)如图2中,取格点D,连接CD,DM.
∵CD∥AN,
∴∠CPN=∠DCM,
∵△DCM是等腰直角三角形,
∴∠DCM=∠D=45°,
∴cos∠CPN=cos∠DCM=![]() .
.
故答案为:2.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
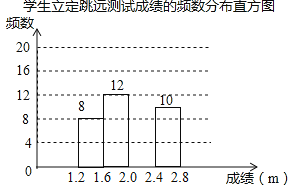
超能学典应用题题卡系列答案【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?