题目内容
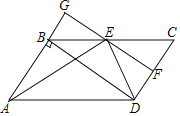
【题目】如图,在平行四边形ABCD中,DB⊥AB,点E是BC边的中点,过点E作EF⊥CD,垂足为F,交AB的延长线于点G.
(1)求证:四边形BDFG是矩形;
(2)若AE平分∠BAD,求tan∠BAE的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据矩形的判定证明即可;
(2)根据平行四边形的性质和等边三角形的性质解答即可.
证明:(1)∵BD⊥AB,EF⊥CD,
∴∠ABD=90°,∠EFD=90°,
根据题意,在ABCD中,AB∥CD,
∴∠BDC=∠ABD=90°,
∴BD∥GF,
∴四边形BDFG为平行四边形,
∵∠BDC=90°,
∴四边形BDFG为矩形;
(2)∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵AD∥BC,
∴∠BEA=∠DAE,
∴∠BAE=∠BEA,
∴BA=BE,
∵在Rt△BCD中,点E为BC边的中点,
∴BE=ED=EC,
∵在ABCD中,AB=CD,
∴△ECD为等边三角形,∠C=60°,
∴![]() ,
,
∴![]() .
.

 智慧小复习系列答案
智慧小复习系列答案【题目】地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识,提高学生生态环境保护意识,举办了“我参与,我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
初二:74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
(1)根据上面的数据,将下列表格补充完整;
整理、描述数据:
成绩x 人数 班级 |
|
|
|
|
|
初一 | 1 | 2 | 3 | 6 | |
初二 | 0 | 1 | 10 | 1 | 8 |
(说明:成绩90分及以上为优秀,80~90分为良好,60~80分为合格,60分以下为不合格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
初一 | 84 | 88.5 | |
初二 | 84.2 | 74 |
(2)得出结论:
你认为哪个年级掌握生态环保知识水平较好并说明理由.(至少从两个不同的角度说明推断的合理性).
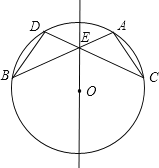
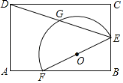
【题目】如图1,AB为半圆O的直径,半径的长为4cm,点C为半圆上一动点,过点C作CE⊥AB,垂足为点E,点D为弧AC的中点,连接DE,如果DE=2OE,求线段AE的长.
小何根据学习函数的经验,将此问题转化为函数问题解决.
小华假设AE的长度为xcm,线段DE的长度为ycm.
(当点C与点A重合时,AE的长度为0cm),对函数y随自变量x的变化而变化的规律进行探究.
下面是小何的探究过程,请补充完整:(说明:相关数据保留一位小数).
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 0 | 1.6 | 2.5 | 3.3 | 4.0 | 4.7 |
| 5.8 | 5.7 |
当x=6cm时,请你在图中帮助小何完成作图,并使用刻度尺度量此时线段DE的长度,填写在表格空白处:
(2)在图2中建立平面直角坐标系,描出补全后的表中各组对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象解决问题,当DE=2OE时,AE的长度约为 cm.

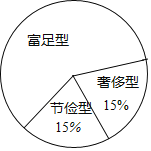
【题目】某校为了解学生每月零用钱情况,从七、八、九年级1200名学生中随机抽取部分学生,对他们今年4月份的零用钱支出情况进行调查统计并绘制成如下统计图表:
组别 | 零用钱支出x(单位:元) | 频数(人数) | 频率 |
节俭型 | x<10 | 2 | 0.05 |
10≤x<20 | 4 | 0.10 | |
富足型 | 20≤x<30 | 12 | |
30≤x<40 | m | ||
奢侈型 | 40≤x<50 | n | |
x≥50 | 2 |
请根据图表中所给的信息,解答下列问题:
(1)在这次调查中共随机抽取了 名学生,图表中的m= ,n= ;
(2)请估计该校今年4月份零用钱支出在“30≤x<40范围的学生人数;
(3)在抽样的“节俭型”学生中,有2位男生和4位女生,校团委计划从中随机抽取两人参与“映山红”的公益活动,求恰好抽中一男一女的概率.