��Ŀ����
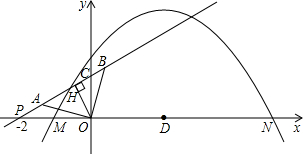
��ͼ��������y=a��x+1����x-5����x��Ľ���ΪM��N��ֱ��y=kx+b��x�ύ��P��-2��0������y�ύ��C����A��B������ֱ��y=kx+b�ϣ���AO=BO=| 2 |
��1��OH�ij��ȵ���
��2���Ƿ����ʵ��a��ʹ��������y=a��x+1����x-5������һ��E��������D��N��EΪ��������������AOB���ƣ��������ڣ�˵�����ɣ������ڣ������з��������������ߵĽ���ʽ��ͬʱ̽������õ����������Ƿ��з���������E�㣨��Ҫ˵�����ɣ�������һ��̽���Է���������ÿһ��
 E�㣬ֱ��NE��ֱ��AB�Ľ���G�Ƿ�������PB•PG��10
E�㣬ֱ��NE��ֱ��AB�Ľ���G�Ƿ�������PB•PG��10| 2 |
��������1������֪�ڵ���ֱ���������н��OH�ij�����ֱ�߹������OH�����ڵ㵽ֱ�߾��룬�����������k��b��
��2��˼άҪ���ܣ����������������DNΪ����ֱ�������ε�ֱ�DZߣ�����DNΪ����ֱ�������ε�б�ߣ�
�������Ƶı�����ϵ�ͼ��ι�ϵ�����ʺϵĸ����ߣ����촹ֱ�Ӷ���֤���Ʊ�����ϵ�Ƿ������
��2��˼άҪ���ܣ����������������DNΪ����ֱ�������ε�ֱ�DZߣ�����DNΪ����ֱ�������ε�б�ߣ�
�������Ƶı�����ϵ�ͼ��ι�ϵ�����ʺϵĸ����ߣ����촹ֱ�Ӷ���֤���Ʊ�����ϵ�Ƿ������
��� �⣺��1����ֱ��y=kx+b��P��-2��0��?-2k+b=0����
�⣺��1����ֱ��y=kx+b��P��-2��0��?-2k+b=0����
��AO=BO=
��AO��BO?������AOBΪ����ֱ�������Σ�
AB=
=2?��OAB=45��?OH=OA��sin45��=1��
��OH=
=1����
�ɢ٢ڷ��̽�ã�k=
��b=
��OH=1��
��2�������ʵ��a��ʹ������y=a��x+1����x-5������һ��E��������D��N��EΪ����������������ֱ�ǡ�AOB���ƣ�
����D��N��EΪ�����������Ϊ����ֱ�������Σ������������������ֻ�����࣬һ������DNΪֱ�DZߵĵ���ֱ�������Σ���һ������DNΪб�ߵĵ���ֱ�������Σ�
����DNΪ����ֱ�������ε�ֱ�DZߣ���ED��DN��
��������y=a��x+1����x-5���У���y=0�����x=-1��5����ã�M��-1��0����N��5��0����
��D��2��0����
��ED=DN=3��
��E��������2��3����
��E��2��3�����������߽���ʽy=a��x+1����x-5�����ã�a��2+1����2-5��=3�����a=-
��
�������߽���ʽΪy=-
��x+1����x-5����
��y=-
x2+
x+
��
����DNΪ����ֱ�������ε�б�ߣ�
��DE��EN��DE=EN��
��E��������3.5��1.5����
��E��3.5��1.5�����������߽���ʽy=a��x+1����x-5���ã�a��3.5+1����3.5-5��=1.5�����a=-
��
�������߽���ʽΪy=-
��x+1����x-5����
��y=-
x2+
x+
��
��a=-
ʱ����������y=-
x2+
x+
�ϴ���һ��E��2��3������������
������������ϻ�������������E�㣬������ΪE��㣬��ôֻ�п��ܡ�DE��N����DNΪб�ߵĵ���ֱ�������Σ�
�ɴ˵�E�䣨3.5��1.5������ȻE�䲻�������ߣ�
y=-
x2+
x+
�ϣ�
���������y=-
x2+
x+
��û�з���������������E�㣮
��a=-
ʱ��ͬ���ɵ�������y=-
x2+
x+
��û�з���������������E�㣮
��E������Ϊ��2��3������Ӧ�������߽���ʽΪy=-
x2+
x+
ʱ��
�ߡ�EDN�͡�ABO���ǵ���ֱ�������Σ�
���GNP=��PBO=45�㣮
�֡ߡ�NPG=��BPO��
���NPG�ס�BPO��
��
=
��
��PB•PG=PO•PN=2��7=14��
��������PB•PG��10
��
��E������Ϊ��3.5��1.5������ö�Ӧ�������߽���ʽΪy=-
x2+
x+
ʱ��
ͬ����֤�ã�PB•PG=PO•PN=2��7=14��
��������PB•PG��10
��
 �⣺��1����ֱ��y=kx+b��P��-2��0��?-2k+b=0����
�⣺��1����ֱ��y=kx+b��P��-2��0��?-2k+b=0������AO=BO=
| 2 |
AB=
| OA2+OB2 |
��OH=
| |b| | ||
|
�ɢ٢ڷ��̽�ã�k=
| ||
| 3 |
2
| ||
| 3 |
��2�������ʵ��a��ʹ������y=a��x+1����x-5������һ��E��������D��N��EΪ����������������ֱ�ǡ�AOB���ƣ�
����D��N��EΪ�����������Ϊ����ֱ�������Σ������������������ֻ�����࣬һ������DNΪֱ�DZߵĵ���ֱ�������Σ���һ������DNΪб�ߵĵ���ֱ�������Σ�
����DNΪ����ֱ�������ε�ֱ�DZߣ���ED��DN��
��������y=a��x+1����x-5���У���y=0�����x=-1��5����ã�M��-1��0����N��5��0����
��D��2��0����
��ED=DN=3��
��E��������2��3����
��E��2��3�����������߽���ʽy=a��x+1����x-5�����ã�a��2+1����2-5��=3�����a=-
| 1 |
| 3 |
�������߽���ʽΪy=-
| 1 |
| 3 |
��y=-
| 1 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
����DNΪ����ֱ�������ε�б�ߣ�
��DE��EN��DE=EN��
��E��������3.5��1.5����
��E��3.5��1.5�����������߽���ʽy=a��x+1����x-5���ã�a��3.5+1����3.5-5��=1.5�����a=-
| 2 |
| 9 |
�������߽���ʽΪy=-
| 2 |
| 9 |
��y=-
| 2 |
| 9 |
| 8 |
| 9 |
| 10 |
| 9 |
��a=-
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
������������ϻ�������������E�㣬������ΪE��㣬��ôֻ�п��ܡ�DE��N����DNΪб�ߵĵ���ֱ�������Σ�
�ɴ˵�E�䣨3.5��1.5������ȻE�䲻�������ߣ�
y=-
| 1 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
���������y=-
| 1 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
��a=-
| 2 |
| 9 |
| 2 |
| 9 |
| 8 |
| 9 |
| 10 |
| 9 |
��E������Ϊ��2��3������Ӧ�������߽���ʽΪy=-
| 1 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
�ߡ�EDN�͡�ABO���ǵ���ֱ�������Σ�
���GNP=��PBO=45�㣮
�֡ߡ�NPG=��BPO��
���NPG�ס�BPO��
��
| PG |
| PO |
| PN |
| PB |
��PB•PG=PO•PN=2��7=14��
��������PB•PG��10
| 2 |
��E������Ϊ��3.5��1.5������ö�Ӧ�������߽���ʽΪy=-
| 2 |
| 9 |
| 8 |
| 9 |
| 10 |
| 9 |
ͬ����֤�ã�PB•PG=PO•PN=2��7=14��
��������PB•PG��10
| 2 |
���������⿼����ֱ���������н��⼼�ɣ�ͨ���ⷽ�������������߽���ʽ���ڶ���̽���������������⣬����˼ά�������ԣ���Ҫ©�����������ѧ��������ۣ�

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��������y=ax2+bx+c��a��0����x����������A��-1��0����B��3��0��������ͼ��֪y��0ʱ��x��ȡֵ��Χ�ǣ�������
��ͼ��������y=ax2+bx+c��a��0����x����������A��-1��0����B��3��0��������ͼ��֪y��0ʱ��x��ȡֵ��Χ�ǣ�������| A��-1��x��3 | B��3��x��-1 | C��x��-1��x��3 | D��x��-1��x��3 |
 26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG|
26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG| ��ͼ�������߽�x���ڵ�A��-2��0������B��4��0������y���ڵ�C��0��4����
��ͼ�������߽�x���ڵ�A��-2��0������B��4��0������y���ڵ�C��0��4���� ��PΪԲ�ĵ�Բ������A��������ֱ��BM���У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��PΪԲ�ĵ�Բ������A��������ֱ��BM���У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ� ����C�ǵ�A���ڵ�B�ĶԳƵ㣬��F���߶�BC���е㣬ֱ��l����F����y��ƽ�У�ֱ��y=-x+m����C����y����D�㣮
����C�ǵ�A���ڵ�B�ĶԳƵ㣬��F���߶�BC���е㣬ֱ��l����F����y��ƽ�У�ֱ��y=-x+m����C����y����D�㣮