题目内容
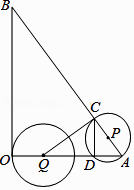
【题目】已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,﹣8),对称轴为x=4.
(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点N以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PN被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点N的运动速度;若不存在,请说明理由;
(3)在(2)的结论下,直线x=1上是否存在点M使△MPN为等腰三角形?若存在,请直接写出所有点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线过C(0,﹣8),
∴c=﹣8,即y=ax2+bx﹣8,
由函数经过点(14,0)及对称轴为x=4可得 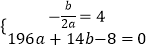 ,
,
解得: 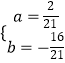 ,
,
∴该抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣8
x﹣8
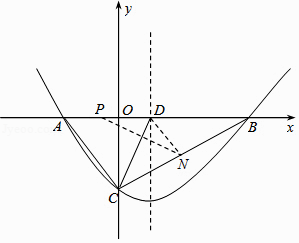
(2)
解:存在直线CD垂直平分PN.
由函数解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣8,可求出点A坐标为(﹣6,0),
x﹣8,可求出点A坐标为(﹣6,0),
在Rt△AOC中,AC= ![]() =
= ![]() =10=AD,
=10=AD,
故可得OD=AD﹣OA=4,点D在函数的对称轴上,
∵线CD垂直平分PN,
∴∠PDC=∠NDC,PD=DN,
由AD=AC可得,∠PDC=∠ACD,
∴∠NDC=∠ACD,
∴DN//AC,
又∵DB=AB﹣AD=20﹣10=10=AD,
∴点D是AB中点,
∴DN为△ABC的中位线,
∴DN= ![]() AC=5,
AC=5,
∴AP=AD﹣PD=AD﹣DN=10﹣5=5,
∴t=5÷1=5(秒),
∴存在t=5(秒)时,线段PN被直线CD垂直平分.
在Rt△BOC中,BC= ![]() =
= ![]() =2
=2 ![]() ,
,
而DN为△ABC的中位线,N是BC中点,
∴CN= ![]() ,
,
∴点N的运动速度为每秒 ![]() 单位长度
单位长度
(3)
解:存在,过点N作NH⊥x轴于H,则NH= ![]() OC=4,
OC=4,
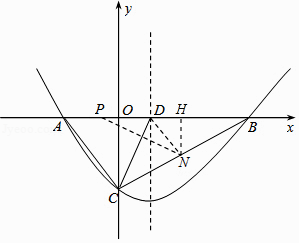
PH=OP+OH=1+7=8,
在Rt△PNH中,PN= ![]() =
= ![]() =4
=4 ![]() ,
,
①当MP=MN,即M为顶点,则此时CD与PN的交点即是M点(上面已经证明CD垂直平分PN),
设直线CD的直线方程为:y=kx+b(k≠0),
因为点C(0,﹣8),点D(4,0),
所以可得直线CD的解析式为:y=2x﹣8,
当x=1时,y=﹣6,
∴M1(1,﹣6);
②当PN为等腰△MPN的腰时,且P为顶点.
设直线x=1上存在点M(1,y),因为点P坐标为(﹣1,0),
从而可得PM2=22+y2,
又PN2=80,
则22+y2=80,
即y=±2 ![]() ,
,
∴M2(1,2 ![]() ),M3(1,﹣2
),M3(1,﹣2 ![]() );
);
③当PN为等腰△MPN的腰时,且N为顶点,点N坐标为(7,﹣4),
设直线x=1存在点M(1,y),
则NM2=62+(y+4)2=80,
解得:y=2 ![]() ﹣4或﹣2
﹣4或﹣2 ![]() ﹣4;
﹣4;
∴M4(1,﹣4+2 ![]() ),M5(1,﹣4﹣2
),M5(1,﹣4﹣2 ![]() ).
).
综上所述:存在这样的五点:M1(1,﹣6),M2(1,2 ![]() ),M3(1,﹣2
),M3(1,﹣2 ![]() ),M4(1,﹣4+2
),M4(1,﹣4+2 ![]() ),M5(1,﹣4﹣2
),M5(1,﹣4﹣2 ![]() ).
).
【解析】(1)由题意抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,﹣8),对称轴为x=4,根据待定系数法可以求得该抛物线的解析式;(2)假设存在,设出时间t,则根据线段PN被直线CD垂直平分,再由垂直平分线的性质及勾股定理来求解t,看t是否存在;(3)假设直线x=1上是存在点M,使△MPN为等腰三角形,此时要分两种情况讨论:①当PN为等腰△MPN的腰时,且P为顶点;②当PN为等腰△MPN的腰时,且Q为顶点;然后再根据等腰三角形的性质及直角三角形的勾股定理求出M点坐标.

【题目】阅读下面材料:
小明想探究函数![]() 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
y | … | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | … |
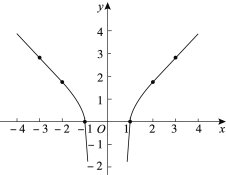
小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是_____________.请写出函数![]() 的一条性质:_____________.
的一条性质:_____________.