题目内容
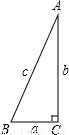
(2003•海南)如图,在Rt△ABC中,a、b分别是∠A、∠B的对边,c为斜边,如果已知两个元素a、∠B,就可以求出其余三个未知元素b、c、∠A.(1)求解的方法有多种,请你按照下列步骤,完成一种求解过程;
(2)请你分别给出a、∠B的一个具体数值,然后按照(1)中的思路,求出b、c、∠A的值.
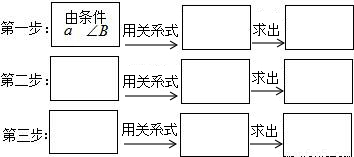
【答案】分析:(1)已知一条直角边和一个锐角,第一步根据两个锐角互余,求得∠A的度数;第二步根据∠B的正切值求得b的长度;第三步根据∠A的余弦值求得斜边c的长度;
(2)可以令a=2,∠B=60°,根据上述思路求解.
解答:解:(1)第一步:根据∠A=90°-∠B,求得∠B;
第二步:根据tanB= ,求得b=atanB;
,求得b=atanB;
第三步:根据cosB= ,求得c=
,求得c=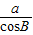 .
.
(2)不妨令a=2,∠B=60°,
则∠A=90°-60°=30°,
∴b=atanB=2 ,
,
c=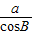 =4.
=4.
点评:此题主要考查了解直角三角形的方法,熟悉有关直角三角形的性质:
(1)勾股定理;
(2)两个锐角互余;
(3)锐角三角函数关系式.
(2)可以令a=2,∠B=60°,根据上述思路求解.
解答:解:(1)第一步:根据∠A=90°-∠B,求得∠B;
第二步:根据tanB=
 ,求得b=atanB;
,求得b=atanB;第三步:根据cosB=
 ,求得c=
,求得c=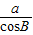 .
.(2)不妨令a=2,∠B=60°,
则∠A=90°-60°=30°,
∴b=atanB=2
 ,
,c=
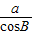 =4.
=4.点评:此题主要考查了解直角三角形的方法,熟悉有关直角三角形的性质:
(1)勾股定理;
(2)两个锐角互余;
(3)锐角三角函数关系式.

练习册系列答案
相关题目
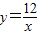 的图象与一次函数y=kx+4的图象相交于P、Q两点,并且P点的纵坐标是6.
的图象与一次函数y=kx+4的图象相交于P、Q两点,并且P点的纵坐标是6.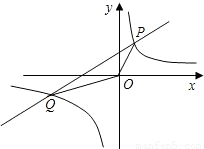
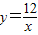 的图象与一次函数y=kx+4的图象相交于P、Q两点,并且P点的纵坐标是6.
的图象与一次函数y=kx+4的图象相交于P、Q两点,并且P点的纵坐标是6.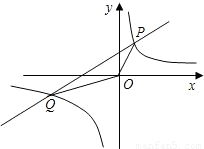
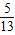 ,则这个菱形的面积是 .
,则这个菱形的面积是 .
 为半圆的
为半圆的 .设扇形AOC、△COB、弓形BmC的面积分别为S1、S2、S3,则下列结论正确的是( )
.设扇形AOC、△COB、弓形BmC的面积分别为S1、S2、S3,则下列结论正确的是( )