题目内容
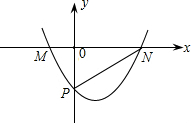 已知二次函数y=ax2+bx+c(a>0)的图象(如图所示)过点M(1-
已知二次函数y=ax2+bx+c(a>0)的图象(如图所示)过点M(1-| 2 |
| 2 |
分析:根据M、N、P的坐标,首先表示出PM2、PN2、MN2的值,由于∠P=90°,利用勾股定理即可求得k的值,从而得到点P的坐标,进而可利用待定系数法求出该抛物线的解析式,也就确定了a、b、c的值.
解答:解:∵△MPN为直角三角形,
∴PM2+PN2=MN2,
∴(1+
)+k2+(1-
)2+k2=[1+
-(1-
)]2,
解得k=±1,
∵k<0,
∴k=-1.
∵抛物线过M,N两点,
设抛物线的关系式为:y=a(x-1-
)(x-1+
),
将(0,-1)代入得,
-1=a(-1-
)(-1+
),
∴a=1,
∴y=(x-1-
)(x-1+
),
∴y=x2-2x-1,
∴a=1,b=-2,c=-1.
∴PM2+PN2=MN2,
∴(1+
| 2 |
| 2 |
| 2 |
| 2 |
解得k=±1,
∵k<0,
∴k=-1.
∵抛物线过M,N两点,
设抛物线的关系式为:y=a(x-1-
| 2 |
| 2 |
将(0,-1)代入得,
-1=a(-1-
| 2 |
| 2 |
∴a=1,
∴y=(x-1-
| 2 |
| 2 |
∴y=x2-2x-1,
∴a=1,b=-2,c=-1.
点评:此题主要考查了二次函数解析式的确定,还涉及到勾股定理的应用,属于基础知识,难度不大.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
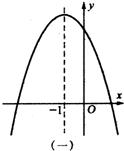 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
