��Ŀ����
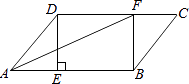
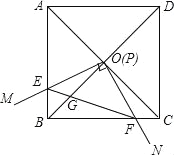
����Ŀ����ͼ���߳�Ϊ1��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����ֱ�ǡ�MPN��ʹֱ�Ƕ���P���O�غϣ�ֱ�DZ�PM��PN�ֱ���OA��OB�غϣ�Ȼ����ʱ����ת��MPN����ת��Ϊ�ȣ�0�㣼�ȣ�90�㣩��PM��PN�ֱ�AB��BC��E��F���㣬����EF��OB�ڵ�G�������н�������ȷ���� ��
��1��EF=![]() OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF=
OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF=![]() OA����4������ת�����У�����BEF����COF�����֮�����ʱ��AE=
OA����4������ת�����У�����BEF����COF�����֮�����ʱ��AE=![]() ����5��OGBD=AE2+CF2��
����5��OGBD=AE2+CF2��
���𰸡���1������2������3������5����
��������
�����������1�����ı���ABCD�������Σ�
��OB=OC����OBE=��OCF=45�㣬��BOC=90�㣬
���BOF+��COF=90�㣬
�ߡ�EOF=90�㣬
���BOF+��COE=90�㣬
���BOE=��COF��
�ڡ�BOE�͡�COF�У�
 ��
��
���BOE�ա�COF��ASA����
��OE=OF��BE=CF��
��EF=![]() OE������ȷ��
OE������ȷ��
��2����S�ı���OEBF=S��BOE+S��BOE=S��BOE+S��COF=S��BOC=![]() S������ABCD��
S������ABCD��
��S�ı���OEBF��S������ABCD=1��4������ȷ��
��3����BE+BF=BF+CF=BC=![]() OA������ȷ��
OA������ȷ��
��4������O��OH��BC��
��BC=1��
��OH=![]() BC=
BC=![]() ��
��
��AE=x����BE=CF=1��x��BF=x��
��S��BEF+S��COF=![]() BEBF+
BEBF+![]() CFOH=
CFOH=![]() x��1��x��+
x��1��x��+![]() ��1��x����
��1��x����![]() =��
=��![]() ��x��
��x��![]() ��2+
��2+![]() ��
��
��a=��![]() ��0��
��0��
�൱x=![]() ʱ��S��BEF+S��COF���
ʱ��S��BEF+S��COF���
������ת�����У�����BEF���COF�����֮�����ʱ��AE=![]() ���ʴ���
���ʴ���
��5���ߡ�EOG=��BOE����OEG=��OBE=45�㣬
���OEG�ס�OBE��
��OE��OB=OG��OE��
��OGOB=OE2��
��OB=![]() BD��OE=
BD��OE=![]() EF��
EF��
��OGBD=EF2��
���ڡ�BEF�У�EF2=BE2+BF2��
��EF2=AE2+CF2��
��OGBD=AE2+CF2������ȷ��