题目内容
学校为了美化校园环境,在一块长40米、宽20米的长方形空地上计划新建一块长9米、宽7米的长方形花圃.(1)若请你在这块空地上设计一个长方形花圃,使它的面积比学校计划新建的长方形花圃的面积多1平方米,请你给出你认为合适的三种不同的方案;
(2)在学校计划新建的长方形花圃周长不变的情况下,长方形花圃的面积能否增加2平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
【答案】分析:(1)本题根据实际有多种不同的方案.
(2)设长方形花圃的长为x米,则宽为16-x.即可列方程,然后根据b2-4ac可知方程有无解.
解答:解:(1)方案1:长为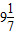 米,宽为7米.(1分)
米,宽为7米.(1分)
方案2:长为9米,宽为7 米.(2分)
米.(2分)
方案3:长=宽=8米;(3分)
(注:本题方案有无数种,写对一个得(1分),共(3分).用图形示意同样给分.)
(2)在长方形花圃周长不变的情况下,长方形花圃面积不能增加2平方米.(4分)
由题意得长方形长与宽的和为16米.
设长方形花圃的长为x米,则宽为(16-x)米.
方法一:x(16-x)=63+2,(5分)
x2-16x+65=0,
∵△=(-16)2-4×1×65=-4<0,
∴此方程无实数根.
∴在周长不变的情况下,长方形花圃的面积不能增加2平方米.(7分)
方法二:S长方形=x(16-x)=-x2+16x(5分)=-(x-8)2+64.
∴在长方形花圃周长不变的情况下,长方形的最大面积为64平方米,因此不能增加2平方米.(7分)
点评:本题考查的是一元二次方程的应用,同时考生要注意考虑实际问题,懂得开放性思考.
(2)设长方形花圃的长为x米,则宽为16-x.即可列方程,然后根据b2-4ac可知方程有无解.
解答:解:(1)方案1:长为
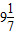 米,宽为7米.(1分)
米,宽为7米.(1分)方案2:长为9米,宽为7
 米.(2分)
米.(2分)方案3:长=宽=8米;(3分)
(注:本题方案有无数种,写对一个得(1分),共(3分).用图形示意同样给分.)
(2)在长方形花圃周长不变的情况下,长方形花圃面积不能增加2平方米.(4分)
由题意得长方形长与宽的和为16米.
设长方形花圃的长为x米,则宽为(16-x)米.
方法一:x(16-x)=63+2,(5分)
x2-16x+65=0,
∵△=(-16)2-4×1×65=-4<0,
∴此方程无实数根.
∴在周长不变的情况下,长方形花圃的面积不能增加2平方米.(7分)
方法二:S长方形=x(16-x)=-x2+16x(5分)=-(x-8)2+64.
∴在长方形花圃周长不变的情况下,长方形的最大面积为64平方米,因此不能增加2平方米.(7分)
点评:本题考查的是一元二次方程的应用,同时考生要注意考虑实际问题,懂得开放性思考.

练习册系列答案
相关题目
 米,宽
米,宽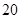 米的长方形空地上计划新建一块长
米的长方形空地上计划新建一块长 米,宽
米,宽 米的长方形花圃.
米的长方形花圃. 平方米,请你给出你认为合适的三种不同的方案;
平方米,请你给出你认为合适的三种不同的方案;
 平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由. 米,宽
米,宽 米的长方形空地上计划新建一块长
米的长方形空地上计划新建一块长 米,宽
米,宽 米的长方形花圃.
米的长方形花圃. 平方米,请你给出你认为合适的三种不同的方案;
平方米,请你给出你认为合适的三种不同的方案;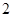
 平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由. 米,宽
米,宽 米的长方形空地上计划新建一块长
米的长方形空地上计划新建一块长 米,宽
米,宽 米的长方形花圃.
米的长方形花圃. 平方米,请你给出你认为合适的三种不同的方案;
平方米,请你给出你认为合适的三种不同的方案; 平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.