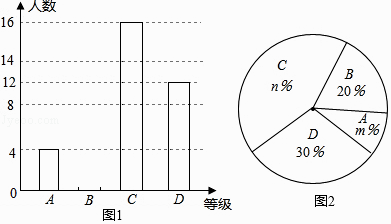
��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+ ![]() x+c��a��0����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C����A������Ϊ��4��0���������ߵĶԳ�����ֱ��x=
x+c��a��0����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C����A������Ϊ��4��0���������ߵĶԳ�����ֱ��x= ![]() ��
��
��1���������ߵĽ���ʽ��
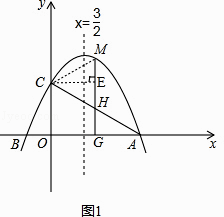
��2��MΪ��һ�����ڵ��������ϵ�һ���㣬����M��MG��x���ڵ�G����AC�ڵ�H�����߶�CM=CHʱ�����M�����ꣻ
��3���ڣ�2���������£����߶�MG�Ƶ�G˳ʱ����תһ���Ǧ���0�㣼����90�㣩������ת�����У����߶�MG�������߽��ڵ�N�����߶�GA���Ƿ���ڵ�P��ʹ����P��N��GΪ��������������ABC���ƣ�������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��x=�� ![]() =
= ![]() ��b=
��b= ![]() ��
��
��a=�� ![]() ��
��
��A��4��0����a=�� ![]() ����y=ax2+
����y=ax2+ ![]() x+c��
x+c��
�ɵã� ![]() ����42+
����42+ ![]() ��4+c=0��
��4+c=0��
���c=2��
�������߽���ʽΪy=�� ![]() x2+
x2+ ![]() x+2
x+2
��2��
�⣺��ͼ1������CM����C����CE��MH�ڵ�E��
 ��
��
��y=�� ![]() x2+
x2+ ![]() x+2��
x+2��
�൱x=0ʱ��y=2��
��C��������ǣ�0��2����
��ֱ��AC����ʽΪy=kx+b��k��0����
��A��4��0����C��0��2������y=kx+b��
�ɵ� ![]() ��
��
��ã� 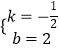 ��
��
��ֱ��AC����ʽΪy=�� ![]() x+2��
x+2��
�ߵ�M���������ϣ���H��AC�ϣ�MG��x�ᣬ
�����M��������m���� ![]() m2+
m2+ ![]() m+2����H��m����
m+2����H��m���� ![]() m+2����
m+2����
��MH=�� ![]() m2+
m2+ ![]() m+2������
m+2������ ![]() m+2��=��
m+2��=�� ![]() m2+2m��
m2+2m��
��CM=CH��OC=GE=2��
��MH=2EH=2��[2������ ![]() m+2��]=m��
m+2��]=m��
�֡�MH=�� ![]() m2+2m��
m2+2m��
�ੁ ![]() m2+2m=m��
m2+2m=m��
��m��m��2��=0��
���m=2��m=0�����������⣬��ȥ����
��m=2��
��m=2ʱ��
y=�� ![]() ��22+
��22+ ![]() ��2+2=3��
��2+2=3��
���M��������2��3��
��3��
�⣺���ڵ�P��ʹ��P��N��GΪ��������������ABC���ƣ�����Ϊ��
����������x�ύ��A��B���㣬A��4��0����A��B�������ֱ��x= ![]() ����Գƣ�
����Գƣ�
��B����1��0����
��AC= ![]() =2
=2 ![]() ��BC=
��BC= ![]() =
= ![]() ��AB=5��
��AB=5��
��AC2+BC2= ![]() +
+ ![]() =25��AB2=52=25��
=25��AB2=52=25��
��AC2+BC2=AB2=25��
���ABCΪֱ�������Σ�
���ACB=90�㣬
�߶�MG��G����ת�����У��������߽��ڵ�N����NP��x��ʱ����NPG=90�㣬
��P��������n��0����
��N��������n���� ![]() n2+
n2+ ![]() n+2����
n+2����
����ͼ2��
�� ![]() =
= ![]() ʱ��
ʱ��
�ߡ�N1P1G=��ACB=90�㣬
���N1P1G�ס�ACB��
�� ![]() =
= ![]() ��
��
��ã�n1=3��n2=��4�����������⣬��ȥ����
��P��������3��0����
�ڵ� ![]() =
= ![]() ʱ��
ʱ��
�ߡ�N2P2G=��BCA=90�㣬
���N2P2G�ס�BCA��
�� ![]() ��
��
��ã�n1=1 ![]() ��n2=1��
��n2=1�� ![]() �����������⣬��ȥ����
�����������⣬��ȥ����
��P��������1+ ![]() ��0����
��0����
����ڵ�P��3��0����1 ![]() ��0����ʹ��P��N��GΪ��������������ABC���ƣ�
��0����ʹ��P��N��GΪ��������������ABC���ƣ�
����������1���������öԳ��ṫʽ���a��ֵ��Ȼ��ѵ�A��������a��ֵ���������ߵĽ���ʽ�����c��ֵ������ȷ���������ߵĽ���ʽ����2�����ȸ��������ߵĽ���ʽȷ������C�����꣬�ٸ��ݴ���ϵ������ȷ����ֱ��AC����ʽΪy=�� ![]() x+2��Ȼ�����M������Ϊ��m����
x+2��Ȼ�����M������Ϊ��m���� ![]() m2+
m2+ ![]() m+2����H��m����
m+2����H��m���� ![]() m+2�������MH��ֵ�Ƕ��٣��ٸ���CM=CH��OC=GE=2���ɵ�MH=2EH���ݴ����m��ֵ�Ƕ��٣��ٰ�m��ֵ���������ߵĽ���ʽ�����y��ֵ������ȷ����M�����꣮��3�������жϳ���ABCΪֱ�������Σ�Ȼ�������������ٵ�
m+2�������MH��ֵ�Ƕ��٣��ٸ���CM=CH��OC=GE=2���ɵ�MH=2EH���ݴ����m��ֵ�Ƕ��٣��ٰ�m��ֵ���������ߵĽ���ʽ�����y��ֵ������ȷ����M�����꣮��3�������жϳ���ABCΪֱ�������Σ�Ȼ�������������ٵ� ![]() =
= ![]() ʱ���ڵ�
ʱ���ڵ� ![]() =
= ![]() ʱ���������������ε����ʣ��жϳ��Ƿ���ڵ�P��ʹ����P��N��GΪ��������������ABC���Ƽ��ɣ�
ʱ���������������ε����ʣ��жϳ��Ƿ���ڵ�P��ʹ����P��N��GΪ��������������ABC���Ƽ��ɣ�

����Ŀ���Ķ�������ϣ�
С����̽������![]() �����ʣ������������������y��x�ļ����Ӧֵ������ƽ��ֱ������ϵ�л����˺���ͼ��
�����ʣ������������������y��x�ļ����Ӧֵ������ƽ��ֱ������ϵ�л����˺���ͼ��
x | �� | -3 | -2 | -1 | 1 | 2 | 3 | �� |
y | �� | 2.83 | 1.73 | 0 | 0 | 1.73 | 2.83 | �� |
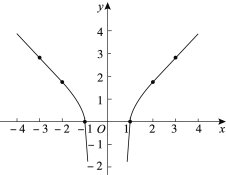
С�Ͽ���һ�۾�˵�����㻭��ͼ��϶��Ǵ���ģ���
��ش�С���жϵ�������_____________����д������![]() ��һ�����ʣ�_____________��
��һ�����ʣ�_____________��