题目内容
将下列正确的命题的序号填在横线上 .①若n为大于2的正整数,则n边形的所有外角之和为(n-2)•180°.
②三角形三条中线的交点就是三角形的重心.
③证明两三角形全等的方法有:SSS,SAS,ASA,SSA及HL等.
【答案】分析:分别根据多边形内角和定理、三角形的重心及全等三角形的判定定理得出结论.
解答:解:①若n为大于2的正整数,则n边形的所有内角之和为(n-2)•180°,故本小题错误;
②三角形三条中线的交点就是三角形的重心,符合重心的定义,故本小题正确;
③SSA不能证明两三角形全等,故本小题错误.
故答案为:②.
点评:本题考查的是多边形内角和定理、三角形的重心及全等三角形的判定定理,熟知以上知识是解答此题的关键.
解答:解:①若n为大于2的正整数,则n边形的所有内角之和为(n-2)•180°,故本小题错误;
②三角形三条中线的交点就是三角形的重心,符合重心的定义,故本小题正确;
③SSA不能证明两三角形全等,故本小题错误.
故答案为:②.
点评:本题考查的是多边形内角和定理、三角形的重心及全等三角形的判定定理,熟知以上知识是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
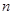 大于2的正整数,则
大于2的正整数,则 .
. 及
及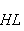 等.
等. 大于2的正整数,则
大于2的正整数,则 边形的所有外角之和为
边形的所有外角之和为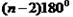 .
. ,
, ,
, ,
, 及
及 等.
等.