Question

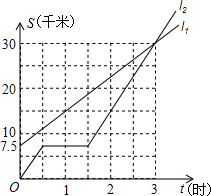如图，l₁、l₂分别表示步行者与骑自行车在同一路上行驶的路程S与时间t的关系．
（1）骑自行车走了一段路后，自行车发生故障，进行修理，所用的时间是

 

小时．
（2）骑车出发后

 

小时与步行者相遇．
（3）若自行车不发生故障，保持出发时的速度前进，

 

小时与步行者相遇．
（4）求出步行者走的路程S与时间t的函数关系式．（写出过程）

Answer 1

分析：（1）由图象上平行于x轴的那一条线段可知修车用了1小时．
（2）由两函数的图象的交点的横坐标可知，答案为3．
（3）未修理车前，步行者的速度是7.5千米/时，自行车的速度是15千米/时，且开始时，步行者多走7.5千米，所以若不发生故障，1小时即可追上．
（4）开始s=at+b，利用图象上的点，结合方程组即可求解．

解答：解：（1）1（2分）

（2）3（2分）

（3）1（2分）

（4）解：设S=ta+b
∵图象过（0，7.5）（3，30）
∴

7.5=b 30=3a+b

．（2分）
解得a=7.5，b=7.5（1分）
∴该函数关系式为S=7.5t+7.5．（1分）

点评：本题只需仔细分析图象，即可求解．