题目内容
(2004•三明)据我国古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得一个直角三角形,如果勾是三、股是四,那么弦就等于五.后人概括为“勾三,股四,弦五”.(1)观察:3,4,5;5,12,13;7,24,25;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.计算
 (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;(2)根据(1)的规律,用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦,合情猜想他们之间二种相等关系并对其中一种猜想加以证明;
(3)继续观察4,3,5;6,8,10;8,15,17;…,可以发现各组的第一个数都是偶数,且从4起也没有间断过.运用类似上述探索的方法,直接用m(m为偶数且m>4)的代数式来表示他们的股和弦.
【答案】分析:(1)根据所提供的例子发现股是勾的平方减去1的二分之一,弦是勾的平方加1的二分之一;
(2)股是勾的平方减去4的四分之一,弦是勾的平方加4的四分之一.
解答:解:(1)∵ (9-1)=4,
(9-1)=4, (9+1)=5;
(9+1)=5; (25-1)=12,
(25-1)=12, (25+1)=13;
(25+1)=13;
∴7,24,25的股的算式为 (49-1)=
(49-1)= (72-1)
(72-1)
弦的算式为 (49+1)=
(49+1)= (72+1);(4分)
(72+1);(4分)
(2)当n为奇数且n≥3,勾、股、弦的代数式分别为:n, (n2-1),
(n2-1), (n2+1).(7分)
(n2+1).(7分)
例如关系式①:弦-股=1;关系式②:勾2+股2=弦2(9分)
证明关系式①:弦-股= (n2+1)-
(n2+1)- (n2-1)=
(n2-1)= [(n2+1)-(n2-1)]=1
[(n2+1)-(n2-1)]=1
或证明关系式②:勾2+股2=n2+[ (n2-1)]2=
(n2-1)]2= n4+
n4+ n2+
n2+ =
= (n2+1)2=弦2∴猜想得证;(12分)
(n2+1)2=弦2∴猜想得证;(12分)
(3)例如探索得,当m为偶数且m>4时,股、弦的代数式分别为: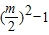 ,
,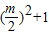 .(14分)
.(14分)
另加分问题,
例如:连接两组勾股数中,上一组的勾、股与下一组的勾的和等于下一组的股.
即上一组为:n, (n2-1),
(n2-1), (n2+1)(n为奇数且n≥3),
(n2+1)(n为奇数且n≥3),
分别记为:A1、B1、C1,
下一组为:n+2, [(n+2)2-1],
[(n+2)2-1], [(n+2)2+1](n为奇数且n≥3),
[(n+2)2+1](n为奇数且n≥3),
分别记为:A2、B2、C2,
则:A1+B1+A2=n+ (n2-1)+(n+2)=
(n2-1)+(n+2)= (n2+4n+3)=
(n2+4n+3)= [(n+2)2-1]=B2.
[(n+2)2-1]=B2.
或B1+C2=B2+C1(证略)等等.
点评:注意由具体例子观察发现规律,证明的时候熟练运用完全平方公式.
(2)股是勾的平方减去4的四分之一,弦是勾的平方加4的四分之一.
解答:解:(1)∵
 (9-1)=4,
(9-1)=4, (9+1)=5;
(9+1)=5; (25-1)=12,
(25-1)=12, (25+1)=13;
(25+1)=13;∴7,24,25的股的算式为
 (49-1)=
(49-1)= (72-1)
(72-1)弦的算式为
 (49+1)=
(49+1)= (72+1);(4分)
(72+1);(4分)(2)当n为奇数且n≥3,勾、股、弦的代数式分别为:n,
 (n2-1),
(n2-1), (n2+1).(7分)
(n2+1).(7分)例如关系式①:弦-股=1;关系式②:勾2+股2=弦2(9分)
证明关系式①:弦-股=
 (n2+1)-
(n2+1)- (n2-1)=
(n2-1)= [(n2+1)-(n2-1)]=1
[(n2+1)-(n2-1)]=1或证明关系式②:勾2+股2=n2+[
 (n2-1)]2=
(n2-1)]2= n4+
n4+ n2+
n2+ =
= (n2+1)2=弦2∴猜想得证;(12分)
(n2+1)2=弦2∴猜想得证;(12分)(3)例如探索得,当m为偶数且m>4时,股、弦的代数式分别为:
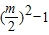 ,
,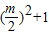 .(14分)
.(14分)另加分问题,
例如:连接两组勾股数中,上一组的勾、股与下一组的勾的和等于下一组的股.
即上一组为:n,
 (n2-1),
(n2-1), (n2+1)(n为奇数且n≥3),
(n2+1)(n为奇数且n≥3),分别记为:A1、B1、C1,
下一组为:n+2,
 [(n+2)2-1],
[(n+2)2-1], [(n+2)2+1](n为奇数且n≥3),
[(n+2)2+1](n为奇数且n≥3),分别记为:A2、B2、C2,
则:A1+B1+A2=n+
 (n2-1)+(n+2)=
(n2-1)+(n+2)= (n2+4n+3)=
(n2+4n+3)= [(n+2)2-1]=B2.
[(n+2)2-1]=B2.或B1+C2=B2+C1(证略)等等.
点评:注意由具体例子观察发现规律,证明的时候熟练运用完全平方公式.

练习册系列答案
相关题目
 (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式; (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式; (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式; (9-1)、
(9-1)、 (9+1)与
(9+1)与 (25-1)、
(25-1)、 (25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;
(25+1),并根据你发现的规律,分别写出能表示7,24,25的股和弦的算式;