题目内容
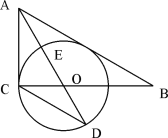
【题目】如图,在Rt△ABC中,∠ACB=90,AO是△ABC的角平分线。以O为圆心,OC为半径作⊙O。
(1)(3分)求证:AB是⊙O的切线。
(2)(3分)已知AO交⊙O于点E,延长AO交⊙O于点D, tanD=![]() ,求
,求![]() 的值。
的值。
(3)(4分)在(2)的条件下,设⊙O的半径为3,求AB的长。
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)过O作OF⊥AB于F,由角平分线上的点到角两边的距离相等即可得证;(2)连接CE,证明△ACE∽△ADC可得![]() = tanD=
= tanD=![]() ;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得
;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得![]() ,设BO=y ,BF=z,列二元一次方程组即可解决问题.
,设BO=y ,BF=z,列二元一次方程组即可解决问题.
试题解析:⑴证明:作OF⊥AB于F
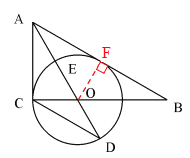
∵AO是∠BAC的角平分线,∠ACB=90
∴OC=OF
∴AB是⊙O的切线
⑵连接CE
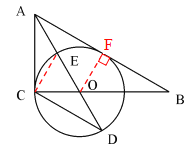
∵AO是∠BAC的角平分线,
∴∠CAE=∠CAD
∵∠ACE所对的弧与∠CDE所对的弧是同弧
∴∠ACE=∠CDE
∴△ACE∽△ADC
∴![]() = tanD=
= tanD=![]()
⑶先在△ACO中,设AE=x,
由勾股定理得
(x+3)=(2x) +3 ,解得x=2,
∵∠BFO=90°=∠ACO
易证Rt△B0F∽Rt△BAC
得![]() ,
,
设BO=y BF=z
![]()
即4z=9+3y,4y=12+3z
解得z=![]() y=
y=![]()
∴AB=![]() +4=
+4=![]()

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目