题目内容
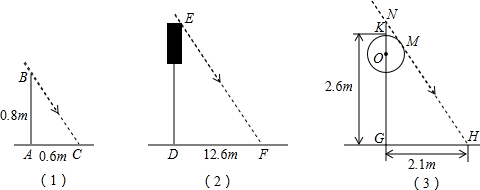
某实验中学甲、乙、丙三个数学兴趣小组制定了一个测量校园物体的方案.于同一时刻在阳光下对标杆及校园中的某些物体进行了测量,下面是他们通过测量得到一些信息:甲组:如图(1),测得一根直立于平地,长为0.8m的标杆的影长为0.6m.
乙组:如图(2),测得学校水塔的影长为12.6m.
丙组:如图(3),测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗线忽略不计)的高度为2.6m,影长为2.1m,
请根据以上信息解答下列问题.
(1)请根据甲、乙两组得到的信息计算出学校水塔的高度.
(2)如图(3),设太阳光NH与圆O相切于点M,请根据甲、丙两组得到的信息,求景灯灯罩的半径.
【答案】分析:(1)根据在同一时刻在阳光下对校园中,学校旗杆与旗杆的影长构成直角三角形Rt△ABC和Rt△DEF相似进行解答即可;
(2)先根据同一时刻物高与影长成正比求出NG的长,再连接OM,由切线的性质可知OM⊥NH,进而可得出△NMO∽△NGH,再根据其对应边成比例列出比例式,然后用半径表示出ON,进行计算即可求出OM的长.
解答:解:(1)因为在同一时刻在阳光下对校园中,学校旗杆与旗杆的影长构成直角三角形Rt△ABC和Rt△DEF,且Rt△ABC∽Rt△DEF,
所以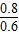 =
=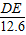 ,
,
所以DE=16.8m;
(2)连接OM,设OM=r,
∵同一时刻物高与影长成正比,
∴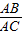 =
=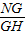 ,
,
即 =
=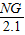 ,
,
解得NG=2.8m,
在Rt△NGH中,NH=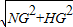 =3.5m,
=3.5m,
设⊙O的半径为r,连接OM,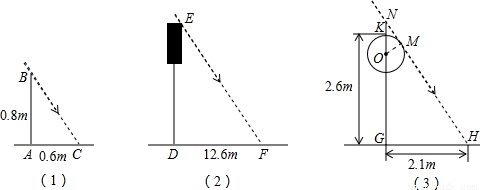
∵MH与⊙O相切于点M,
∴OM⊥NH,
∴∠NMO=∠NGH=90°,
又∠ONM=∠GNH,
∴△NMO∽△NGH,
∴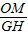 =
=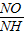 ,
,
即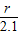 =
=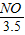 ,
,
又NO=NK+KO=(NG-KG)+KO=2.8-2.1+r=0.7+r,
则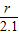 =
=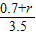 .
.
∴3.5r=2.1(0.7+r),
解得r=1.05m.
点评:此题考查的是相似三角形在实际生活中的运用,解答此类题目的关键是根据相似三角形的判定定理得出相似的三角形,再根据相似三角形的性质解答.
(2)先根据同一时刻物高与影长成正比求出NG的长,再连接OM,由切线的性质可知OM⊥NH,进而可得出△NMO∽△NGH,再根据其对应边成比例列出比例式,然后用半径表示出ON,进行计算即可求出OM的长.
解答:解:(1)因为在同一时刻在阳光下对校园中,学校旗杆与旗杆的影长构成直角三角形Rt△ABC和Rt△DEF,且Rt△ABC∽Rt△DEF,
所以
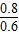 =
=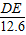 ,
,所以DE=16.8m;
(2)连接OM,设OM=r,
∵同一时刻物高与影长成正比,
∴
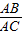 =
=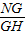 ,
,即
 =
=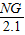 ,
,解得NG=2.8m,
在Rt△NGH中,NH=
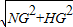 =3.5m,
=3.5m,设⊙O的半径为r,连接OM,

∵MH与⊙O相切于点M,
∴OM⊥NH,
∴∠NMO=∠NGH=90°,
又∠ONM=∠GNH,
∴△NMO∽△NGH,
∴
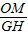 =
=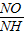 ,
,即
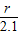 =
=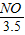 ,
,又NO=NK+KO=(NG-KG)+KO=2.8-2.1+r=0.7+r,
则
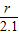 =
=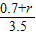 .
.∴3.5r=2.1(0.7+r),
解得r=1.05m.
点评:此题考查的是相似三角形在实际生活中的运用,解答此类题目的关键是根据相似三角形的判定定理得出相似的三角形,再根据相似三角形的性质解答.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目